【题目】如图,四边形ABCD中,∠ADC=∠ABC=90°,与∠ADC、∠ABC相邻的两外角平分线交于点E,若∠A=50°,则∠E的度数为( )

A. 60°B. 50°C. 40°D. 30°
参考答案:
【答案】C
【解析】
运用四边形的内角和等于360°,可求∠DCB的度数,再利用角平分线的性质及三角形的外角性质可求∠E的度数.
解:如图,连接EC并延长,
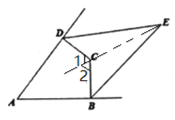
∵∠ADC=∠ABC=90°,∠A=50°,
∴∠DCB=360°-90°-90°-50°=130°,
∵∠ADC、∠ABC相邻的两外角平分线交于点E,
∴∠CDE=∠CBE=45°,
∵∠1=∠CDE+∠DEC,∠2=∠CBE+∠BEC
即∠DCB=∠CDE+∠CBE+∠BED=130°,
∴∠BED=130°-45°-45°=40°.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图ΔABC中,AB=AC,D点在BC上,且BD=AD,DC=AC.并求∠B的度数.
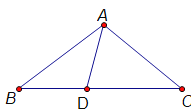
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=60°,∠C=40°,P,Q分别在BC,CA上,AP,BQ分别是∠BAC,∠ABC的角平分线.求证:BQ+AQ=AB+BP.
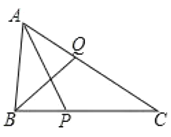
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F.
(1)求证:∠CDB=∠BFD;
(2)若AB=10,AC=8,求DF的长.
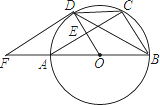
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某农场有A、B两种型号的收割机共20台,每台A型收割机每天可收大麦100亩或者小麦80亩,每台B型收割机每天可收大麦80亩或者小麦60亩,该农场现有19 000亩大麦和11 500亩小麦先后等待收割.先安排这20台收割机全部收割大麦,并且恰好10天时间全部收完.
(1)问A、B两种型号的收割机各多少台?
(2)由于气候影响,要求通过加班方式使每台收割机每天多完成10%的收割量,问这20台收割机能否在一周时间内完成全部小麦收割任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD,如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为16
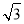 米,加固后大坝的横截面为梯形ABED,CE的长为8米.
米,加固后大坝的横截面为梯形ABED,CE的长为8米.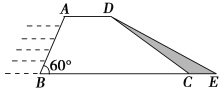
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE的坡度.
相关试题

