【题目】已知:如图所示,在△ABC中,∠C=90°,BC=5cm,AC=7cm.两个动点P、Q分别从B、C两点同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
(1)P、Q两点在运动过程中,经过几秒后,△PCQ的面积等于4厘米2?经过几秒后PQ的长度等于5厘米?
(2)在P、Q两点在运动过程中,四边形ABPQ的面积能否等于11厘米2?试说明理由.
(3)经过几秒时以C、P、Q为顶点的三角形与△ABC相似?

参考答案:
【答案】(1) 经过1秒后,其面积等于4厘米2,当经过0秒或2秒后PQ=5;(2) 四边形ABPQ的面积不能等于11厘米2,理由见解析;(3)经过![]() 或
或![]() 秒后两三角形相似,理由见解析
秒后两三角形相似,理由见解析
【解析】试题分析:(1)若使其面积为4,即S△PCQ=![]() PCQC=4,代入数据求解即可;设经过t秒后PQ=5.由PC2+CQ2=PQ2,代入求解即可;
PCQC=4,代入数据求解即可;设经过t秒后PQ=5.由PC2+CQ2=PQ2,代入求解即可;
(2)若四边形ABPQ的面积能等于11,即S△PCQ=![]() ﹣11=
﹣11=![]() ,建立方程,解方程看是否有解,若有,则存在;
,建立方程,解方程看是否有解,若有,则存在;
(3)要使三角形相似,其对应边成比例即可.
试题解析:解:(1)可设经x秒后其面积为4,即![]() ×(5﹣x)×2x=4,解得:x=1或x=4.
×(5﹣x)×2x=4,解得:x=1或x=4.
当x=4时,2x=8>7,舍去.∴x=1.
设经过t秒后PQ=5.∵PC2+CQ2=PQ2.∵PC=5﹣t,CQ=2t,PQ=5,∴(5﹣t)2+(2t)2=52,解得:t=0或2,∴当经过0秒或2秒后PQ=5.
答:经过1秒后,其面积等于4厘米2,经过0秒或2秒后PQ=5.
(2)若四边形ABPQ的面积能等于11厘米2,即S△PCQ=![]() ﹣11=
﹣11=![]() ,即
,即![]() ×(5﹣x)×2x=
×(5﹣x)×2x=![]() ,化简得:2x2﹣10x+13=0,△=b2﹣4ac=10×10﹣4×2×13<0,所以此方程无解.
,化简得:2x2﹣10x+13=0,△=b2﹣4ac=10×10﹣4×2×13<0,所以此方程无解.
故四边形ABPQ的面积不能等于11厘米2.
(3)若两个三角形相似,①当PQ∥AB时,有![]() ,解得:x=
,解得:x=![]() .
.
②当PQ不平行AB时,有![]() ,解得:x=
,解得:x=![]() .
.
即经过![]() 或
或![]() 秒后两三角形相似.
秒后两三角形相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则原方程化为y2﹣5y+4=0,解此方程得:y1=1,y2=4.
当y=1时,x2﹣1═1,∴x=±
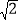 .
.当y=4时,x2﹣1═4,∴x=±
 .
.∴原方程的解为:x1=
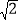 ,x2=﹣
,x2=﹣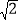 ,x3=
,x3= ,x4=﹣
,x4=﹣ .
.以上方法叫做换元法解方程,达到了降次的目的,体现了转化思想.
运用上述方法解方程:x4﹣8x2+12=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
 (2)-5.6+0.9-4.4+8.1﹣0.1
(2)-5.6+0.9-4.4+8.1﹣0.1(3)
 ; (4)
; (4)
(5)
 (6)
(6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长10cm,宽8cm的长方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)要使无盖长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)如果把长方形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的长方形,然后折合成一个有盖的长方体盒子,那么它的侧面积(指的是高为剪去的正方形边长的长方体的侧面积)可以达到30cm2吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同数字的卡片,请按要求抽出卡片,完成下列各问题:

(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?答:我抽取的2张卡片是________、________,乘积的最大值为________.
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?答:我抽取的2张卡片是________、________,商的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成下列的相似测试.
如图,在△ABC中,AB=AC=4,D是AB上一点,且BD=1,连接CD,然后作∠CDE=∠B,交平行于BC且过点A的直线于点E,DE交AC于点F,连接CE.
(1)求证:△AFD∽△EFC;
(2)试求AEBC的值.

相关试题

