Question

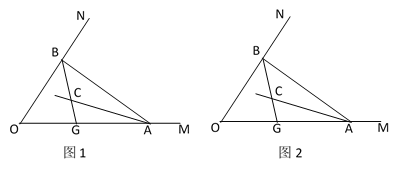
【题目】如图1，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．

（1）若∠MON＝60°，则∠ACG＝ °；若∠MON＝90°，则∠ACG＝ °；

（2）若∠MON＝n°，请求出∠ACG的度数；（用含n的代数式表示）

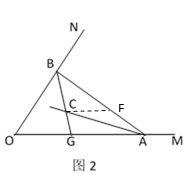
（3）如图2，若∠MON＝n°，过C作直线与AB交于F，若CF∥OA时，求∠BGO－∠ACF的度数．（用含n的代数式表示）．

Answer 1

【答案】（1）60°；45°；（2）90°－n；（3）90°－n．

【解析】

（1）根据三角形的内角和求出∠ABO+∠BAO的度数，再根据角平分线的定义及外角的性质即可得到∠ACG的度数；

（2）根据（1）中的结论即可求出答案；

（3）根据角平分线的性质，平行线的性质得到∠ACF=∠CAO=∠BAC，利用外角的性质得到∠BGO－∠ACF=∠ACG，由此得到答案.

（1）∵∠MON+∠ABO+∠BAO＝180°，

∴∠ABO+∠BAO=180°-∠MON，

∵AC、BC分别是∠BAO和∠ABO的角平分线，

∴∠ABC=∠ABO，∠BAC=∠BAO，

当∠MON＝60°，

∠ACG=∠ABC+∠BAC=(∠ABO+∠BAO)=（180°-∠MON）=60°，

当∠MON＝90°，

∠ACG=∠ABC+∠BAC=(∠ABO+∠BAO)=（180°-∠MON）=45°，

故答案为：60°，45°；

（2）由（1）知∠ACG=（180°-∠MON），

∵∠MON＝n°，

∴∠ACG=（180°-∠MON）=90°－n；

（3）∵AC平分∠BAO，

∴∠BAC=∠CAO

∵CF∥OA，

∴∠ACF=∠CAO=∠BAC，

∵∠BGO=∠ABG+∠BAO=∠ABG+2∠ACF,

∴∠BGO－∠ACF=∠ABG+2∠ACF-∠ACF=∠ABG+∠ACF=∠ABG+∠BAC=∠ACG,

∵∠MON＝n°时∠ACG=90°－n，

∴∠BGO－∠ACF=90°－n.