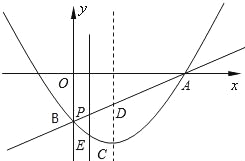
【题目】如图,抛物线的顶点为C(1,﹣2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(1)求直线AB的解析式.
(2)设点P的横坐标为x,求点E的坐标(用含x的代数式表示).
(3)求△ABE面积的最大值.
参考答案:
【答案】(1)直线AB解析式为y=![]() x﹣
x﹣![]() ;
;
(2)E点的坐标为(x, ![]() x2﹣x﹣
x2﹣x﹣![]() );
);
(3)△ABE面积的最大值为![]() .
.
【解析】试题分析:(1)由条件可先求得抛物线解析式,则可求得B点坐标,再利用待定系数法可求得直线AB解析式;
(2)由条件可知P、E的横坐标相同,又点E在抛物线上,则可表示出E点坐标;
(3)由(2)可用x表示出PE的长,则可用x表示出△ABE的面积,再利用二次函数的性质可求得其最大值.
试题解析:(1)∵抛物线顶点坐标为(1,﹣2),
∴可设抛物线解析式为y=a(x﹣1)2﹣2,
∵OA=3,且点A在x轴的正半轴上,
∴A(3,0),
∴0=a(3﹣1)2﹣2,解得a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣1)2﹣2=
(x﹣1)2﹣2=![]() x2﹣x﹣
x2﹣x﹣![]() ,当x=0时可得y=﹣
,当x=0时可得y=﹣![]() ,
,
∴B(0,﹣![]() ),
),
设直线AB解析式为y=kx+b,把A、B坐标代入可得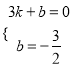 ,解得
,解得 ,
,
∴y=![]() x﹣
x﹣![]() ;
;
(2)∵点P为线段AB上的一个动点,且PE⊥x轴,
∴点E的横坐标为x,
∵点E在抛物线上,
∴E点的坐标为(x, ![]() x2﹣x﹣
x2﹣x﹣![]() );
);
(3)∵点P为线段AB上的一点,
∴P(x, ![]() x﹣
x﹣![]() ),则E(x,
),则E(x, ![]() x2﹣x﹣
x2﹣x﹣![]() ),
),
∴PE=![]() x﹣
x﹣![]() ﹣(
﹣(![]() x2﹣x﹣
x2﹣x﹣![]() )=﹣
)=﹣![]() x2+
x2+![]() x,
x,
由(2)可知点B到PE的距离x,点A以PE的距离为3﹣x,
∴S△ABE=![]() PEx+
PEx+![]() PE(3﹣x)=
PE(3﹣x)=![]() PE(x+3﹣x)=
PE(x+3﹣x)=![]() PE=
PE=![]() (﹣
(﹣![]() x2+
x2+![]() x)=﹣
x)=﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当x=![]() 时,S△ABE有最大值,最大值为
时,S△ABE有最大值,最大值为![]() ,
,
∴△ABE面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,则下列不等式变形错误的是( )
A.a+1 < b+1
B. <
< 
C.3a-4>3b-4
D.4-3a>4-3b -
科目: 来源: 题型:
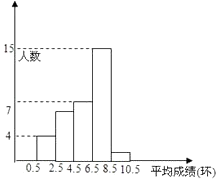
查看答案和解析>>【题目】为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计,分别绘制了如下统计表和频率分布直方图,请你根据统计表和频率分布直方图回答下列问题:
平均成绩
0
1
2
3
4
5
6
7
8
9
10
人数
0
1
3
3
4
6
1
0
(1)参加这次射击比赛的队员有多少名?
(2)这次射击比赛平均成绩的中位数落在频率分布直方图的哪个小组内?
(3)这次射击比赛平均成绩的众数落在频率分布直方图的哪个小组内? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,个位数字是 2,若十位上的数字为 a,则这个两位数可表示为_____.
-
科目: 来源: 题型:
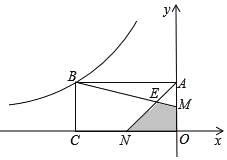
查看答案和解析>>【题目】如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )
A. y=﹣
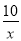 B. y=﹣
B. y=﹣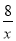 C. y=﹣
C. y=﹣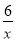 D. y=﹣
D. y=﹣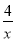
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式组
 的整数解共有4个,则a的取值范围是 ( )
的整数解共有4个,则a的取值范围是 ( )
A.6<a<7
B.6≤a<7
C.6≤a≤7
D.6<a≤7 -
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC各顶点的纵坐标加“﹣3”,连接这三点所成的三角形是由△ABC( )
A. 向上平移3个单位得到的 B. 向下平移3个单位得到的
C. 向左平移3个单位得到的 D. 向右平移3个单位得到的
相关试题

