【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y= ![]() 交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.
交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.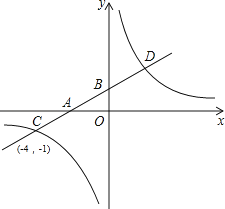
(1)求反比例函数与一次函数的解析式;
(2)若点P为坐标轴上一点,且S△ACP=2S△ABO , 请直接写出点P的坐标.
参考答案:
【答案】
(1)
解:∵点C坐标为(﹣4,﹣1)在反比例函数y= ![]() 的图象上,
的图象上,
∴﹣1= ![]() ,
,
解得:n=4,
∴反比例函数的解析式为:y= ![]() ;
;
∵点D的横坐标为2,
∴y= ![]() =2,
=2,
∴点D(2,2),
将点C与D代入一次函数解析式,可得: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式的解析式为:y= ![]() x+1;
x+1;
(2)
解:如图

∵一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,
∴A(﹣2,0),B(0,1),
∴S△ABO= ![]() ×2×1=1,
×2×1=1,
∴S△ACP=2S△ABO=2,
若点P在x轴上,则AP=4,
∴点P的坐标为:(﹣6,0)或(2,0),
若点P在y轴上,则S△ACP=S△BCP﹣S△ABP= ![]() ×4×BP﹣
×4×BP﹣ ![]() ×BP×2=2,
×BP×2=2,
∴BP=2,
∴点P(0,3)或(0,﹣1).
综上可得:点P的坐标为:(﹣6,0),(2,0),(0,3)或(0,﹣1).
【解析】(1)由一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y= ![]() 交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2,利用待定系数法即可求得反比例函数与一次函数的解析式;(2)分别从点P在x轴上与在y轴上,去分析求解即可求得答案.
交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2,利用待定系数法即可求得反比例函数与一次函数的解析式;(2)分别从点P在x轴上与在y轴上,去分析求解即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟
0<x≤5
5<x≤10
10<x≤15
15<x≤20
频数(通话次数)
20
16
9
5
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BF,∠1与∠2互补.
(1)试说明:FG∥AB;
(2)若∠CFG=60°,∠2=150°,则DE与AC垂直吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校门前正对一条公路,车流量较大,为便于学生安全通过,特建一座人行天桥.如图,是这座天桥的引桥部分示意图,上桥通道由两段互相平行的楼梯AB、CD和一段平行于地面的平台CB构成.已知∠A=37°,天桥高度DH为5.1米,引桥水平跨度AH为8.3米.
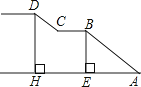
(1)求水平平台BC的长度;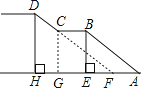
(2)若两段楼梯AB:CD=10:7,求楼梯AB的水平宽度AE的长.
(参考数据:sin37°≈ ,cos37°≈
,cos37°≈ 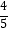 ,tan37°≈
,tan37°≈  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了庆祝即将到来的“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段
频数
频率
60≤x<70
30
0.15
70≤x<80
m
0.45
80≤x<90
60
n
90≤x≤100
20
0.1
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩80≤x<100范围内的学生有多少人?

-
科目: 来源: 题型:
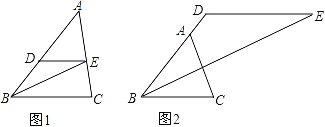
查看答案和解析>>【题目】在△ABC中,点D在边BA或BA的延长线上,过点D作DE∥BC,交∠ABC的角平分线于点E.
(1)如图1,当点D在边BA上时,点E恰好在边AC上,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由.
相关试题

