【题目】乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题: 
(1)乙车休息了h.
(2)求乙车与甲车相遇后y乙关于x的函数表达式,并写出自变量x的取值范围.
(3)当两车相距40km时,求x的值.
参考答案:
【答案】
(1)0.5
(2)解:设乙车与甲车相遇后y乙关于x的函数表达式为:y乙=k1x+b1,
y乙=k1x+b1图象过点(2.5,200),(5,400),
得 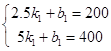 ,
,
解得 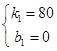 ,
,
乙车与甲车相遇后y乙与x的函数解析式y乙=80x;
(3)解:设乙车与甲车相遇前y乙与x的函数解析式y乙=kx,图象过点(2,200),
解得k=100,
∴乙车与甲车相遇前y乙与x的函数解析式y乙=100x,
0≤x<2.5,y甲减y乙等于40千米,
即400﹣80x﹣100x=40,解得 x=2;
2.5≤x≤5时,y乙减y甲等于40千米,
即2.5≤x≤5时,80x﹣(﹣80x+400)=40,解得x= ![]() ,
,
综上所述:x=2或x= ![]() .
.
【解析】解:(1)设甲车与B地的距离y(km)与行驶时间x(h)之间的函数关系式为y=kx+b,
可得: ![]() ,
,
解得: ![]() .
.
所以函数解析式为:y=﹣80x+400;
把y=200代入y=﹣80x+400中,可得:200=﹣80x+400,
解得:x=2.5,
所以乙车休息的时间为:2.5﹣2=0.5小时;
所以答案是:0.5;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,对角线BD长为18cm,P是AB上任意一点,则点P到AC、BD的距离之和等于cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【感知】如图①,四边形ABCD、CEFG均为正方形,可知BE=DG.
【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F,求证:BE=DG.
【应用】如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上,若AE=2ED,∠A=∠F,△EBC的面积为6,则菱形CEFG的面积为 .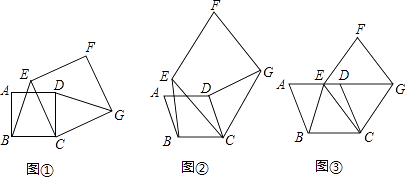
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:-a3-ab2+2a2b=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50min,然后将调查数据整理,作出如图15所示的频数直方图的一部分.

(1)补全频数直方图;
(2)该班学生在路上花费的时间在哪个范围内最多?
(3)该班学生上学路上花费时间在30min以上(含30min)的人数占全班人数的百分比是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b都是实数,且满足(2﹣a)2+|b﹣4|=0,ax2+bx﹣8=0.求式子x2+2x的算术平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.如果两个角相等,那么这两个角是对顶角
B.两直线被第三条直线所截,所得的内错角相等
C.两平行线被第三条直线所截,同位角相等
D.经过一点有且只有一条直线与已知直线平行
相关试题

