【题目】如图,在矩形ABCD中,已知 AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=2,AE =3,AD=7,求线段AF的长.

参考答案:
【答案】(1)见解析;(2)AF=6.
【解析】
(1)由四边形ABCD为矩形,于是得到∠A=∠D=90°,根据垂直的定义得到∠AEF+∠DEC=90°,于是得到∠F=∠DEC,即可得到结论;
(2)由四边形ABCD为矩形,得到DC=AB=2,求出ED=AD-AE=4,根据相似三角形的性质得到![]() ,代入数据即可得到结论.
,代入数据即可得到结论.
(1)∵四边形ABCD为矩形,
∴∠A =∠D =90°.
∵CE⊥EF,
∴∠AEF+∠DEC =90°.
又∵∠F+∠AEF=90°,
∴∠F=∠DEC.
∴△AEF∽△DCE.
(2)∵四边形ABCD为矩形,
∴DC=AB=2.
∵AE =3,AD=7,
∴ED= AD-AE=4.
∵△AEF∽△DCE,
∴![]() .
.
∴![]() .
.
∴AF=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车100辆,但由于种种原因,实际每天的销售量与计划量相比有出入。下表是某周的销售情况(超额记为正、不足记为负):
星期
一
二
三
四
五
六
日
与计划量的差值
+4
-3
-5
+14
-8
+21
-6
(1)根据记录的数据可知该店前三天共销售该品牌儿童滑板车______辆。
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______辆。
(3)该店实行每日计件工资制,每销售一辆车可得40元,若超额完成任务,则超过部分每辆另奖15元;少销售一辆扣20元,那么该店铺的销售人员这一周的工资总额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),点B(4,0),与y轴的交点为C
(1)求二次函数的关系式;
(2)已知点M是线段OB上一动点,过点M作平行于y轴的直线l,直线l与抛物线交于点E,与直线BC交于点F,连接CE,若△CEF与△OBC相似,求点M的坐标;
(3)已知点M是x轴正半轴上一动点,过点M作平行于y轴的直线l,直线l与抛物线交于P,与直线BC交于点Q,连接CP,将△CPQ沿CP翻折后,是否存在这样的直线l,使得翻折后的点Q刚好落在y轴上?若存在,请求出此时点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张等宽的纸条交叉叠放在一起,若重叠都分构成的四边形ABCD中,AB=3,BD=4.则AC的长为_________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点
 ,点
,点 分别表示数
分别表示数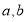 ,则线段
,则线段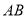 的长度可以用
的长度可以用 表示.
表示.例如:在数轴上点
 表示5,点
表示5,点 表示2,则线段
表示2,则线段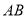 的长表示为
的长表示为 .
.(1)若线段
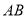 的长表示为6,
的长表示为6, ,则
,则 的值等于____________;
的值等于____________;(2)已知数轴上的任意一点
 表示的数是
表示的数是 ,且
,且 的最小值是4,若
的最小值是4,若 ,则
,则 ____________;
____________;(3)已知点
 在点
在点 的右边,且
的右边,且 ,若
,若 ,
, ,试判断
,试判断 的符号,说明理由.
的符号,说明理由. -
科目: 来源: 题型:
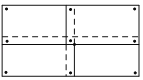
查看答案和解析>>【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如用9枚图钉将4张作品钉在墙上如图).若有28枚图钉可供选用,则最多可以展示绘画作品( )
A. 16张B. 18张C. 20张D. 21张
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为打造智慧课堂,准备集体购买一批平板电脑,原计划订购60台,每台1000元,商家表示,如果多购,可以优惠,结果校长实际订购了72台,每台减价30元,但商家获得同样多的利润.
(1)求每台平板电脑的成本是多少元?
(2)求商家的利润是多少元?
相关试题

