【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如用9枚图钉将4张作品钉在墙上如图).若有28枚图钉可供选用,则最多可以展示绘画作品( )
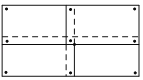
A. 16张B. 18张C. 20张D. 21张
参考答案:
【答案】B
【解析】
分别找出展示的绘画作品展示成一行、二行、三行、四行、五行的时候,28枚图钉最多可以展示的画的数量,比较后即可得出结论.
解:①如果所有的画展示成一行,28÷(1+1)﹣1=13(张),
∴28枚图钉最多可以展示13张画;
②如果所有的画展示成两行,28÷(2+1)=9……1(枚),
9﹣1=8(张),2×8=16(张),
∴28枚图钉最多可以展示16张画;
③如果所有的画展示成三行,28÷(3+1)=7,
7﹣1=6,3×6=18(张),
∴28枚图钉最多可以展示18张画;
④如果所有的画展示成四行,28÷(4+1)=5……3(枚),
5﹣1=4(张),4×4=16(张),
∴28枚图钉最多可以展示16张画;
⑤如果所有的画展示成五行,28÷(5+1)=4,
4﹣1=3(张),5×3=15(张),
∴28枚图钉最多可以展示15张画.
综上所述:28枚图钉最多可以展示18张画.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张等宽的纸条交叉叠放在一起,若重叠都分构成的四边形ABCD中,AB=3,BD=4.则AC的长为_________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,已知 AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=2,AE =3,AD=7,求线段AF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点
 ,点
,点 分别表示数
分别表示数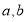 ,则线段
,则线段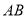 的长度可以用
的长度可以用 表示.
表示.例如:在数轴上点
 表示5,点
表示5,点 表示2,则线段
表示2,则线段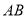 的长表示为
的长表示为 .
.(1)若线段
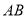 的长表示为6,
的长表示为6, ,则
,则 的值等于____________;
的值等于____________;(2)已知数轴上的任意一点
 表示的数是
表示的数是 ,且
,且 的最小值是4,若
的最小值是4,若 ,则
,则 ____________;
____________;(3)已知点
 在点
在点 的右边,且
的右边,且 ,若
,若 ,
, ,试判断
,试判断 的符号,说明理由.
的符号,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为打造智慧课堂,准备集体购买一批平板电脑,原计划订购60台,每台1000元,商家表示,如果多购,可以优惠,结果校长实际订购了72台,每台减价30元,但商家获得同样多的利润.
(1)求每台平板电脑的成本是多少元?
(2)求商家的利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )种
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)图中的t1= 分;
(2)若乙提速后,乙登山的速度是甲登山的速度的3倍,
①则甲登山的速度是 米/分,图中的t2= 分;
②请求出乙登山过程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.

相关试题

