【题目】直线AB∥CD,EF分别交AB、CD于点M、N,NP平分∠MND. 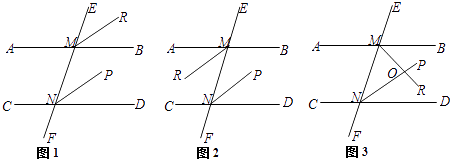
(1)如图1,若MR平分∠EMB,则MR∥NP.请你把下面的解答过程补充完整: 解:因为AB∥CD(已知)
所以∠EMB=∠END()
因为MR平分∠EMB,NP平分∠MND(已知)
所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)
∠MND(角平分线定义)
所以∠EMR=∠MNP
所以MR∥NP()
(2)如图2,若MR平分∠AMN,则MR与NP又怎样的位置关系?请在横线上写出你的猜想结论:;
(3)如图3,若MR平分∠BMN,则MR与NP又怎样的位置关系?请说明理由.
参考答案:
【答案】
(1)两直线平行,同位角相等;同位角相等,两直线平行
(2)MR∥NP
(3)解:MR⊥NP;理由如下:
因为AB∥CD,
所以∠BMN+∠MND=180°,
因为MR平分∠BMN,NP平分∠MND,
所以∠RMN= ![]() ∠BMN,∠MNP=
∠BMN,∠MNP= ![]() ∠MND,
∠MND,
所以∠RMN+∠MNP= ![]() (∠BMN+∠MND)=90°,
(∠BMN+∠MND)=90°,
所以∠MON=90°,
所以MR⊥NP
【解析】解:(1)因为AB∥CD(已知)所以∠EMB=∠END(两直线平行,同位角相等)因为MR平分∠EMB,NP平分∠MND(已知)所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)所以∠EMR=∠MNP所以MR∥NP(同位角相等,两直线平行)所以答案是:两直线平行,同位角相等;同位角相等,两直线平行; (2)MR∥NP;理由如下:因为AB∥CD(已知)所以∠AMN=∠MND(两直线平行,内错角相等)因为MR平分∠AMN,NP平分∠MND(已知)所以∠NMR=
∠MND(角平分线定义)所以∠EMR=∠MNP所以MR∥NP(同位角相等,两直线平行)所以答案是:两直线平行,同位角相等;同位角相等,两直线平行; (2)MR∥NP;理由如下:因为AB∥CD(已知)所以∠AMN=∠MND(两直线平行,内错角相等)因为MR平分∠AMN,NP平分∠MND(已知)所以∠NMR= ![]() ∠AMN,∠MNP=
∠AMN,∠MNP= ![]() ∠MND(角平分线定义)所以∠NMR=∠MNP所以MR∥NP(内错角相等,两直线平行)所以答案是:MR∥NP;
∠MND(角平分线定义)所以∠NMR=∠MNP所以MR∥NP(内错角相等,两直线平行)所以答案是:MR∥NP;
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=2x+1向下平移3个单位长度后所得直线的解析式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长37米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?如图是两位学生争议的情境:请根据上面的信息,解决问题:
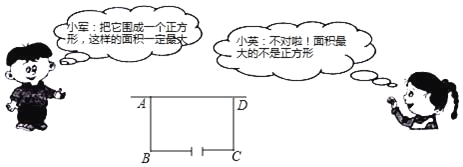
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“同角的余角相等”改写成“如果…那么…”的形式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程2(2x﹣1)=3x+1与关于x的方程2ax=(a+1)x-6的解相同,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A的坐标为(3,-2),则点A向右平移3个单位后的坐标为( )
A. (0,-2) B. (6,-2) C. (3,1) D. (3,-5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8)
B.(1,﹣2)
C.(﹣6,﹣1)
D.(0,﹣1)
相关试题

