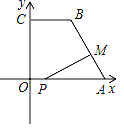
【题目】如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?
参考答案:
【答案】(1)10;(2)中点处;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)过点![]() 作
作![]() 轴于点
轴于点![]() ,利用勾股定理求出
,利用勾股定理求出![]() 的长度;
的长度;
(2)先判断出点![]() 在
在![]() 上,然后表示出
上,然后表示出![]() 即可用三角形的面积公式即可;
即可用三角形的面积公式即可;
(3)![]() 为直角三角形时,由于没有规定哪个顶点是直角顶点,所以分三种情况进行讨论;利用锐角三角函数或相似三角形的性质即可.
为直角三角形时,由于没有规定哪个顶点是直角顶点,所以分三种情况进行讨论;利用锐角三角函数或相似三角形的性质即可.
试题解析:
(1)如图1,过点B作BD⊥x轴于点D,
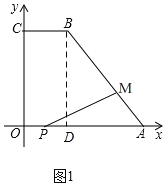
∵A(10,0),B(4,8)C(0,8),
∴AO=10,BD=8,AD=6,
由勾股定理可求得:AB=10,
(2)∵AB=10,
∴10÷2=5,
![]()
∴点M在AB上,
作ME⊥OA于E,
∴△AEM∽△ADB,
![]()
![]()
![]()
![]()
![]()
∴t=5时,S取最大值,此时PA=10t=5,
即:点P在OA的中点处.
(3)由题意可知:![]()
当点P是直角顶点时,
∴PM⊥AP,
∴PA=10t,
若![]() 时,点M在AB上,如图2,
时,点M在AB上,如图2,
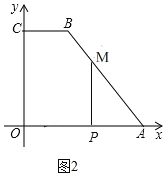
此时AM=2t,
![]()
![]()
![]()
若![]() 时,点M在BC上,如图3,
时,点M在BC上,如图3,
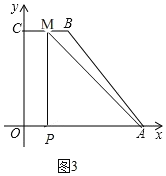
∴CM=142t,OP=t,
∴OP=CM,
∴t=142t,
![]() 当点A是直角顶点时,
当点A是直角顶点时,
此时,∠MAP不可能为![]() 此情况不符合题意;
此情况不符合题意;
当点M是直角顶点时,
若![]() 时,M在AB上,如图4,
时,M在AB上,如图4,
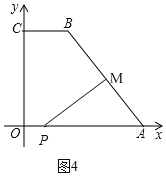
此时,AM=2t,AP=10t
![]()
![]()
![]()
![]()
若![]() 时,点M在BC上,如图5,
时,点M在BC上,如图5,
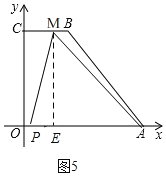
过点M作ME⊥x轴于点E,
此时,CM=142t,OP=t,
∴ME=8,PE=CMOP=143t,
∴EA=10(142t)=2t4,
![]()
![]()
∴∠PME=∠MAP,
∴△PME∽△MAE,
![]()
![]()
∴64=(143t)(2t4),
![]()
![]() 故此情况不存在;
故此情况不存在;
综上所述,t=![]() 或
或![]()
-
科目: 来源: 题型:
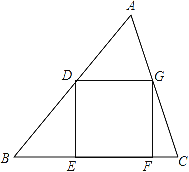
查看答案和解析>>【题目】已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将直角三角形ACB,
 ,AC=6,沿CB方向平移得直角三角形DEF,BF=2,DG=
,AC=6,沿CB方向平移得直角三角形DEF,BF=2,DG= ,阴影部分面积为_______.
,阴影部分面积为_______.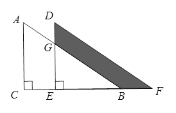
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
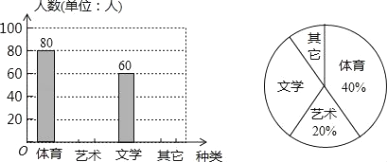
(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红和小凤两人在解关于
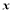 、
、 的方程组
的方程组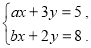 时,小红只因看错了系数
时,小红只因看错了系数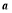 ,得到方程组的解为
,得到方程组的解为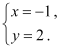 ;小凤只因看错了系数
;小凤只因看错了系数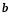 ,得到方程组的解为
,得到方程组的解为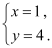 ;求
;求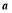 、
、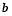 的值和原方程组的解.
的值和原方程组的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数

100
150
200
500
800
1000
摸到白球的次数

58
96
116
295
484
601
摸到白球的频率

0.58
0.64
0.58
0.59
0.605
0.601
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:
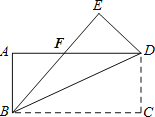
①BD=AD2+AB2;②△ABF≌△EDF;③
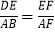 ;④AD=BD cos45°.其中正确的一组是( )
;④AD=BD cos45°.其中正确的一组是( )A. ①② B. ②③ C. ①④ D. ③④
相关试题

