【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为 . 
参考答案:
【答案】4.8
【解析】解:如图所示:
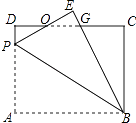
∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
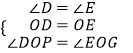 ,
,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6﹣x,DG=x,
∴CG=8﹣x,BG=8﹣(6﹣x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8﹣x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8;
故答案为:4.8.
根据菱形的性质,得到对边相等,四角相等,得到△ODP≌△OEG,根据全等三角形的性质,得到对应边、对应角相等,由边、角相等得到△ODP≌△OEG,根据勾股定理求出AP的值.
-
科目: 来源: 题型:
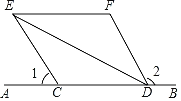
查看答案和解析>>【题目】已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)求证:CE∥DF;
(2)若∠DCE=126°,求∠DEF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件:(1)∠A=25°,∠B=65°;(2)3∠A=2∠B=∠C;(3)∠A=5∠B;(4)2∠A=3∠B=4∠C中,其中能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.

(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(m-1)x2+(m+1)x+3m-1=0,当m_________时,是一元一次方程;当m_________时,是一元二次方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)判断下列未知数的值是不是方程2x2+x-1=0的根.
x1=-1,x2=1,x3=
 .
.(2)已知m是方程x2-x-2=0的一个根,求代数式m2-m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市上网有两种收费方案,用户可任选其一,A为计时制--1元
 时;B为包月制--80元
时;B为包月制--80元 月,此外每种上网方式都附加通讯费
月,此外每种上网方式都附加通讯费 元
元 时.
时. 某用户每月上网40小时,选哪种方式比较合适?
某用户每月上网40小时,选哪种方式比较合适? 某用户每月有100元钱用于上网,选哪种方式比较合算?
某用户每月有100元钱用于上网,选哪种方式比较合算? 请你设计一个方案,使用户能合理地选择上网方式.
请你设计一个方案,使用户能合理地选择上网方式.
相关试题

