【题目】如图,AB分别是⊙O的直径,AC是弦,DC是⊙O的切线,C为切点,AD⊥DC于点D.
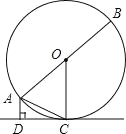
(1)已知∠ACD=a,求∠AOC的大小;
(2)求证:AC2=AB·AD.
参考答案:
【答案】(1)2α;(2)证明见解析.
【解析】
试题分析:(1)由CD是⊙O的切线得到∠OCD=90°,即∠ACD+∠ACO=90°,利用OC=OA得到∠ACO=∠CAO,然后利用三角形的内角和即可证明题目的结论;
(2)如图,连接BC.由AB是直径得到∠ACB=90°,然后利用已知条件可以证明在Rt△ACD∽Rt△ABC,接着利用相似三角形的性质即可解决问题.
试题解析:(1)∵CD是⊙O的切线,
∴∠OCD=90°,
即∠ACD+∠ACO=90°,①
∵OC=OA,
∴∠ACO=∠CAO,
∴∠AOC=180°-2∠ACO,即∠AOC+2∠ACO=180°,
两边除以2得:![]() ∠AOC+∠ACO=90°,②
∠AOC+∠ACO=90°,②
由①,②,得:∠ACD-![]() ∠AOC=0,
∠AOC=0,
即∠AOC=2∠ACD=2α;
(2)如图,连接BC.
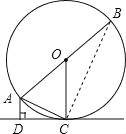
∵AB是直径,
∴∠ACB=90°,
在Rt△ACD与Rt△ABC中,
∵∠AOC=2∠B,
∴∠B=∠ACD,
∴Rt△ACD∽Rt△ABC,
∴![]() ,即AC2=AB·AD.
,即AC2=AB·AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列四个数中,在-3到0之间的数是( )
A. -2.8 B. -3.14 C. -4 D. -4.13
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一几何图形放在平面镜前,则该图形与镜子里的图形全等,因为它们的________________相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.
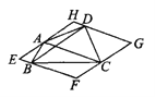
(1)当四边形ABCD分别是菱形、矩形、平行四边形时,相应的四边形EFGH一定是“平行四边形、菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:

(2)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时,相应的原四边形ABCD必须满足怎样的条件?
当 时,四边形EFGH是矩形;当 时四边形EFGH是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
①bc>0;
②2a-3c<0;
③2a+b>0;
④ax2+bx+c=0有两个解x1,x2,当x1>x2时,x1>0,x2<0;
⑤a+b+c>0;
⑥当x>1时,y随x增大而减小.

A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E在BC上,且CE=
 BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=
BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF= S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )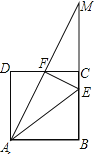
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2-4x-3的顶点坐标是_____________.
相关试题

