【题目】已知抛物线![]() 的图象与
的图象与![]() 轴有两个公共点.
轴有两个公共点.
(1)求![]() 的取值范围,写出当
的取值范围,写出当![]() 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为![]() ,
,
①求![]() 的顶点
的顶点![]() 的坐标;
的坐标;
②若当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的值;
的值;
(3)将![]() 平移得到抛物线
平移得到抛物线![]() ,使
,使![]() 的顶点
的顶点![]() 落在以原点为圆心半径为
落在以原点为圆心半径为![]() 的圆上,求点
的圆上,求点![]() 与
与![]() 两点间的距离最大时
两点间的距离最大时![]() 的解析式,怎样平移
的解析式,怎样平移![]() 可以得到所求抛物线?
可以得到所求抛物线?

参考答案:
【答案】(1)![]() ;(2) ①
;(2) ①![]() ,②1;(3)
,②1;(3)![]() 的解析式为
的解析式为![]() .将抛物线记为
.将抛物线记为![]() 向左平移
向左平移![]() ,再向上平移
,再向上平移![]() 即可得到抛物线
即可得到抛物线![]() .
.
【解析】试题分析:(1)函数图形与x轴有两个公共点,则该函数为二次函数且△>0,故此可得到关于m的不等式组,从而可求得m的取值范围;
(2)①把(1)中求得的函数解析式改为顶点式,即可得出顶点P的坐标;
②先求得抛物线的对称轴,当1≤x≤n时,函数图象位于对称轴的右侧,y随x的增大而增大,当x=n时,y有最大值2n,然后将x=n,y=2n代入求解即可;
(3)由弦的性质可得当PQ经过圆心时,PQ有最大值,此时Q点位于第二象限.根据点P、O的坐标,求得直线OP的解析式,设出点Q的坐标,根据点Q在直线PO上,以及点Q到原点的距离是![]() 即可求出点Q的坐标,进而得出C2的解析式,得出C2如何由C1平移得到.
即可求出点Q的坐标,进而得出C2的解析式,得出C2如何由C1平移得到.
试题解析:
解:(1)由题意可得: 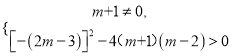 ,
,
解得: ![]() 且
且![]()
当![]() 取最大整数时,其值为2,此时函数解析式为:
取最大整数时,其值为2,此时函数解析式为: ![]() .
.
(2)①由![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
②抛物线C1的对称轴为![]() ,
,
∴当![]() 时,
时, ![]() 随
随![]() 的增大而增大.
的增大而增大.
∵当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
(3)由弦的性质,当线段![]() 经过圆心
经过圆心![]() 时,
时, ![]() 距离最大,此时点
距离最大,此时点![]() 位于第二象限.
位于第二象限.
由![]() ,
, ![]() 可求得直线
可求得直线![]() 的解析式为:
的解析式为: ![]() ,
,
设![]() ,PQ在直线
,PQ在直线![]() 上,
上, ![]() ,
,
圆![]() 半径为
半径为![]() ,
, ![]() ,
,
解之得![]() (舍去)或者
(舍去)或者![]() ,故
,故![]() .
.
∴![]() 的解析式为:
的解析式为: ![]() .
.
将抛物线记为![]() 向左平移
向左平移![]() 再向上平移
再向上平移![]() 即可得到抛物线记为
即可得到抛物线记为![]() .
.
-
科目: 来源: 题型:
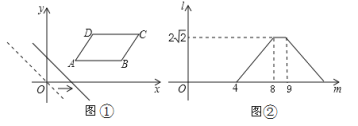
查看答案和解析>>【题目】如图①,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②所示,那么AD的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2(k+1)x+k2﹣2k﹣3与x轴有两个交点.
(Ⅰ)求k取值范围;
(Ⅱ)当k取最小整数时,此二次函数的对称轴和顶点坐标;
(Ⅲ)将(Ⅱ)中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象.请你求出新图象与直线y=x+m有三个不同公共点时m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】家乐福超市“端午节”举行有奖促销活动:凡一次性购物满200元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三等奖,奖金依次为48元、40元、32元.一次性购物满200元者,如果不摇奖可返还现金15元.
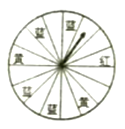
(1)摇奖一次,获一等奖的概率是多少?
(2)小明一次性购物满了200元,他是参与摇奖划算还是领15元现金划算,请你帮他算算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:小刚站在河边的
 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树 处,接着再向前走了30步到达
处,接着再向前走了30步到达 处,然后他左转
处,然后他左转 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点
 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且
 于D,与⊙O交于点F.
于D,与⊙O交于点F.(1)判断AC是否是∠DAE的平分线?并说明理由;
(2)连接OF与AC交于点G,当AG=GC=1时,求切线
 的长.
的长.
相关试题

