【题目】如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且![]() 于D,与⊙O交于点F.
于D,与⊙O交于点F.
(1)判断AC是否是∠DAE的平分线?并说明理由;
(2)连接OF与AC交于点G,当AG=GC=1时,求切线![]() 的长.
的长.

参考答案:
【答案】(1) AC是∠DAE的平分线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接OC,根据切线的性质可得OC⊥DE,又AD⊥DE,得出AD∥OC,根据圆的半径相等得出∠1=∠OCA,再由平行线的性质得出∠2=∠OCA,等量代换即可得出结论;
(2)先证明△AOF是等边三角形,进而得出∠DAO=60°,由(1)中结论可得∠1=30°,根据直角三角形的两锐角互余可得∠E=30°,所以∠1=∠E,根据等角对等边得出CE=AC,即可得到答案.
试题解析:
解:(1)AC是∠DAE的平分线.
证明:连接![]() .
.
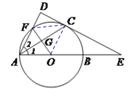
∵DE是⊙O的切线,∴OC⊥DE,.
∵AD⊥DE,∴∠ADC=∠OCE=![]() ,
,
∴AD∥OC,.
∴∠2=∠ACO,∵OA=OC,∴∠1=∠ACO,
∴∠1=∠2,∴AC是∠DAE的平分线.
(2)∵![]() =1 , ∴
=1 , ∴![]() ,即
,即![]() .
.
又∠1=∠2, ![]()
![]() , ∴
, ∴![]()
又![]() ,
, ![]() ∴△
∴△![]() 是等边三角形,
是等边三角形,
![]() ,
, ![]() ,.
,.
又∠ADE=![]() ,
,
∴![]() .
.
∴CE=AC=AG+CG=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
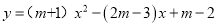 的图象与
的图象与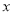 轴有两个公共点.
轴有两个公共点.(1)求
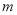 的取值范围,写出当
的取值范围,写出当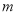 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;(2)将(1)中所求得的抛物线记为
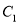 ,
,①求
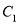 的顶点
的顶点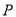 的坐标;
的坐标;②若当
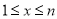 时,
时,  的取值范围是
的取值范围是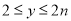 ,求
,求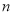 的值;
的值;(3)将
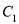 平移得到抛物线
平移得到抛物线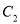 ,使
,使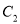 的顶点
的顶点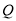 落在以原点为圆心半径为
落在以原点为圆心半径为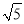 的圆上,求点
的圆上,求点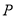 与
与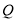 两点间的距离最大时
两点间的距离最大时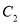 的解析式,怎样平移
的解析式,怎样平移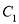 可以得到所求抛物线?
可以得到所求抛物线?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:小刚站在河边的
 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树 处,接着再向前走了30步到达
处,接着再向前走了30步到达 处,然后他左转
处,然后他左转 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点
 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P与点Q都在y轴上,且关于x轴对称.
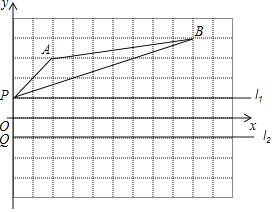
(1)请画出△ABP关于x轴的对称图形△A′B′Q(其中点A的对称点用A′表示,点B的对称点用B′表示);
(2)点P、Q同时都从y轴上的位置出发,分别沿l1、l2方向,以相同的速度向右运动,在运动过程中是否在某个位置使得AP+BQ=A′B成立?若存在,请你在图中画出此时PQ的位置(用线段P′Q′表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“国庆”期间,某电影院装修后重新开业,试营业期间统计发现,影院每天售出的电影票张数y(张)与电影票售价
 (元/张)之间满足一次函数关系:
(元/张)之间满足一次函数关系:  ,
, 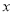 是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入
是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入 运营成本).
运营成本).(1)试求w与
 之间的函数关系式;
之间的函数关系式; (2)影院将电影票售价定为多少时,每天获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
相关试题

