【题目】已知二次函数y=x2﹣2(k+1)x+k2﹣2k﹣3与x轴有两个交点.
(Ⅰ)求k取值范围;
(Ⅱ)当k取最小整数时,此二次函数的对称轴和顶点坐标;
(Ⅲ)将(Ⅱ)中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象.请你求出新图象与直线y=x+m有三个不同公共点时m的值.

参考答案:
【答案】(Ⅰ)k>﹣1(Ⅱ)对称轴为:x=1.顶点坐标为(1,﹣4);(Ⅲ)m的值为1或![]()
【解析】试题分析:(Ⅰ)由抛物线与x轴有两个交点可知△>0,从而可求得k的取值范围;
(Ⅱ)先求得k的最小整数值,从而可求得二次函数的解析式,结合函数解析式求此二次函数的对称轴和顶点坐标;
(Ⅲ)先根据函数解析式画出图形,然后结合图形找出抛物线与x轴有三个交点的情形,最后求得直线的解析式,从而可求得m的值.
试题解析:(Ⅰ)∵抛物线与x轴有两个交点,
∴△=4(k+1)2﹣4(k2﹣2k﹣3)=16k+16>0,
∴k>﹣1,
∴k的取值范围为k>﹣1;
(Ⅱ)∵k>﹣1,且k取最小的整数,
∴k=0,
∴y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴对称轴为:x=1.顶点坐标为(1,﹣4);
(Ⅲ)翻折后所得新图象如图所示,

平移直线y=x+m知:直线位于l1和l2时,它与新图象有三个不同的公共点,
①当直线位于l1时,此时l1过点A(﹣1,0),
∴0=﹣1+m,即m=1;
②∵当直线位于l2时,此时l2与函数y=﹣x2+2x+3(﹣1≤x≤3)的图象有一个公共点,
∴方程x+m=﹣x2+2x+3,即x2﹣x﹣3+m=0有两个相等实根,
∴△=1﹣4(m﹣3)=0,即m=![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从
 地出发,匀速驶向
地出发,匀速驶向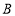 地.甲车以
地.甲车以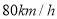 的速度行驶
的速度行驶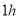 后,乙车才沿相同路线行驶.乙车先到达
后,乙车才沿相同路线行驶.乙车先到达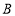 地并停留
地并停留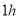 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离
后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离 与乙车行驶时间
与乙车行驶时间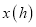 之间的函数关系如图所示.下列说法:①乙车的速度是
之间的函数关系如图所示.下列说法:①乙车的速度是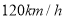 ;②
;②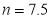 ;③点
;③点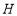 的坐标是
的坐标是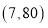 ;④
;④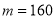 .其中说法正确的是_________.
.其中说法正确的是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量
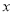 的取值范围;
的取值范围;(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,将□ABCD放置在第一象限,且AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②所示,那么AD的长为__________.
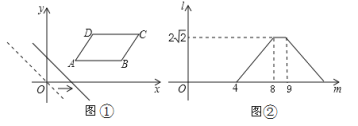
-
科目: 来源: 题型:
查看答案和解析>>【题目】家乐福超市“端午节”举行有奖促销活动:凡一次性购物满200元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三等奖,奖金依次为48元、40元、32元.一次性购物满200元者,如果不摇奖可返还现金15元.
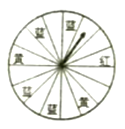
(1)摇奖一次,获一等奖的概率是多少?
(2)小明一次性购物满了200元,他是参与摇奖划算还是领15元现金划算,请你帮他算算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
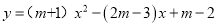 的图象与
的图象与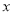 轴有两个公共点.
轴有两个公共点.(1)求
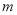 的取值范围,写出当
的取值范围,写出当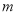 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;(2)将(1)中所求得的抛物线记为
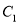 ,
,①求
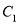 的顶点
的顶点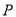 的坐标;
的坐标;②若当
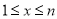 时,
时,  的取值范围是
的取值范围是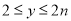 ,求
,求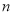 的值;
的值;(3)将
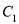 平移得到抛物线
平移得到抛物线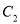 ,使
,使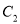 的顶点
的顶点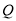 落在以原点为圆心半径为
落在以原点为圆心半径为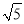 的圆上,求点
的圆上,求点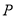 与
与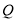 两点间的距离最大时
两点间的距离最大时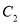 的解析式,怎样平移
的解析式,怎样平移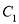 可以得到所求抛物线?
可以得到所求抛物线?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:小刚站在河边的
 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树 处,接着再向前走了30步到达
处,接着再向前走了30步到达 处,然后他左转
处,然后他左转 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点
 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由.
相关试题

