【题目】某公路检修队乘车从A地出发,在南北走向的公路上检修道路,规定向南走为正,向北走为负,从出发到收工时所行驶的路程记录如下(单位:千米):+2,+5,+7,+6,-8,-8,-7,+12.
(1)问收工时,检修队在A地哪边,距A地多远?
(2)问从出发到收工时,汽车共行驶多少千米?
(3)在汽车行驶过程中,若每行驶l千米耗油![]() 升,则检修队从A地出发到回到A地,汽车共耗油多少升?
升,则检修队从A地出发到回到A地,汽车共耗油多少升?
参考答案:
【答案】(1)收工时,检修队在A地的南边9公里处;(2)从出发到收工时,汽车共行驶了55公里;(3)检修队从A地出发到回到A地,汽车共耗油10.24升.
【解析】
(1)将“+2,+5,+7,+6,-8,-8,-7,+12”进行有理数加法运算即可;
(2)将“+2,+5,+7,+6,-8,-8,-7,+12”的绝对值相加即可;
(3)根据“耗油量=路程×每千米耗油量”即可得.
(1)![]()
所以,收工时,检修队在A地的南边9公里处;
(2)![]()
所以,从出发到收工时,汽车共行驶了55公里;
(3)![]() (升)
(升)
所以,则检修队从A地出发到回到A地,汽车共耗油10.24升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一直角三角板
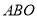 的直角顶点
的直角顶点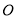 在直线
在直线 上,作射线
上,作射线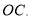 三角板的各边和射线
三角板的各边和射线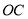 都处于直线
都处于直线 的上方.
的上方.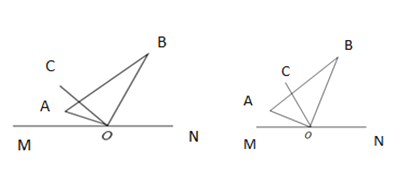
(1)将三角板绕
 点在平面内旋转,当
点在平面内旋转,当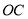 平分
平分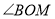 时,如图1,如果
时,如图1,如果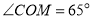 ,求
,求 的度数;
的度数;(2)如图2,将三角板
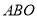 绕
绕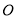 点在平面内任意转动,如果
点在平面内任意转动,如果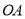 始终在
始终在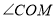 内,且
内,且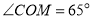 ,请问:
,请问: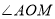 和
和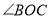 有怎样的数量关系?
有怎样的数量关系?(3)如图2,如果
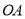 平分
平分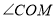 ,
,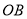 是否也平分
是否也平分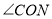 ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段话,并解决后面的问题 .观察下面一例数:
1,2,4,8,……
我们发现,这一列数从第2项起,每一项与它前一项的比都等于2 .
一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数叫做等比数列的公比 .
(1)等比数列5,-15,45,……的第4项是 ;
(2)如果一列数
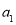 ,
,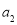 ,
,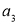 ,
,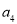 ,……是等比数列,且公比为q,那么根据上述的规定,有
,……是等比数列,且公比为q,那么根据上述的规定,有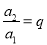 ,
,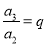 ,
,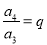 ,……
,……所以
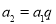 ,
,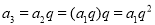 ,
,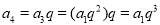 ,
,……
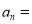 .(用
.(用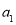 与q的代数式表示)
与q的代数式表示)(3)一个等比数列的第2项是10,第3项是20,求它的第1项与第4项 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为建设国家森林城市,园林部门决定搭配A.B两种园艺造型共50个摆放在市区,现有3490盆甲种花卉和2950盆乙种花卉可供使用,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的费用是800元,搭配一个B种造型的费用是960元,试说明(1)中哪种方案费用最低?最低费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为_______(只添加一个条件即可);

-
科目: 来源: 题型:
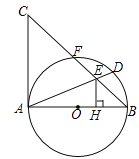
查看答案和解析>>【题目】如图,已知AB为⊙O直径,AC是⊙O的切线,连接BC交⊙O于点F,取
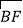 的中点D,连接AD交BC于点E,过点E作EH⊥AB于H.
的中点D,连接AD交BC于点E,过点E作EH⊥AB于H.(1)求证:△HBE∽△ABC;
(2)若CF=4,BF=5,求AC和EH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间接到一批限期(可以提前)完成的零件加工任务.如果每天加工150个,则恰好按期完成;如果每天加工200个,则可比原计划提前5天完成.
(1)求这批零件的个数;
(2)车间按每天加工200个零件的速度加工了
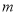 个零件后,提高了加工速度,每天加工250个零件,结果比原计划提前6天完成了生产任务,求
个零件后,提高了加工速度,每天加工250个零件,结果比原计划提前6天完成了生产任务,求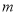 的值.
的值.
相关试题

