【题目】已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.
(1)求抛物线的表达式;
(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,
求tan∠CPA的值;
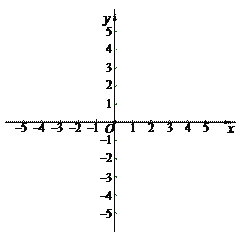
(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E的坐标;若不存在,请说明理由.
参考答案:
【答案】 (1)![]() ;(2)
;(2) ![]() ;(3)E的坐标为(-2,-4)或(4,-4).
;(3)E的坐标为(-2,-4)或(4,-4).
【解析】试题分析:(1)把A、B两点带入抛物线解析式,求得a、b的值,即可得到抛物线解析式;
(2)由AC=AB且点C在点A的左侧,及线段CP是线段CA、CB的比例中项,可得CP=![]() ,
,
由两边对应成比例且夹角相等的三角形相似,可得△CPA∽△CBP,由此∠CPA= ∠CBP.
过P作PH⊥x轴于H,易得PH=4,H(-7,0),BH=12. 由于P(-7,-4),可求![]() ;
;
(3)分两种情况:点E在M左侧和点E在M右侧讨论即可.
试题解析:(1)∵ 抛物线![]() 与x轴交于点A(1,0),B(5,0),
与x轴交于点A(1,0),B(5,0),
∴![]() ,
,
解得![]()
∴ 抛物线的解析式为![]() .
.
(2)∵ A(1,0),B(5,0),
∴ OA=1,AB=4.
∵ AC=AB且点C在点A的左侧,
∴ AC=4 .
∴ CB=CA+AB=8.
∵ 线段CP是线段CA、CB的比例中项,
∴ ![]() .
.
∴ CP=![]() .
.
又 ∵ ∠PCB是公共角,
∴ △CPA∽△CBP .
∴ ∠CPA= ∠CBP.
过P作PH⊥x轴于H.
∵ OC=OD=3,∠DOC=90°,
∴ ∠DCO=45°.∴ ∠PCH=45°
∴ PH=CH=CP![]() =4,
=4,
∴ H(-7,0),BH=12,
∴ P(-7,-4),
∴![]() ,
,
tan∠CPA=![]() .
.
(3) ∵ 抛物线的顶点是M(3,-4),
又 ∵ P(-7,-4),
∴ PM∥x轴 .
当点E在M左, 则∠BAM=∠AME.
∵ ∠AEM=∠AMB,
∴ △AEM∽△BMA.
∴![]() ,
,
∴![]() .
.
∴ ME=5,∴ E(-2,-4).
过点A作AN⊥PM于点N,则N(1,-4).
当点E在M右侧时,记为点![]() ,
,
∵ ∠A![]() N=∠AEN,
N=∠AEN,
∴ 点![]() 与E 关于直线AN对称,则
与E 关于直线AN对称,则![]() (4,-4).
(4,-4).
综上所述,E的坐标为(-2,-4)或(4,-4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在锐角△ABC中,CE⊥AB于点E,点D在边AC上,联结BD交CE于点F,且EF·FC=FB·DF.
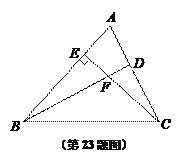
(1)求证:BD⊥AC;
(2)联结AF,求证:AF·BE=BC·EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若|a|=-b,|b|=b,则a=b=0;②若-a不是正数,则a为非负数;③|-a
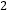 |=(-a)
|=(-a)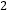 ; ④若
; ④若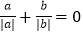 ,则
,则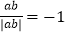 ; ⑤若a+b=0,则a3+b3=0; ⑥若|a|>b,则a2>b2;其中正确的结论有( )
; ⑤若a+b=0,则a3+b3=0; ⑥若|a|>b,则a2>b2;其中正确的结论有( )A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.
(1)求甲、乙每天能生产多少万只口罩?
(2)问至少应安排两个工厂工作多少天才能完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司要生产若干件新产品,需要加工后才能投放市场.现有红星和巨星两个工厂都想加工这批产品,已知红星厂单独加工这批产品比巨星厂单独加工多用20天,红星厂每天可以加工16个,巨星厂每天可以加工24个.公司需付红星厂每天加工费80元,巨星厂每天加工费120元.
(1)这家公司要生产多少件新产品?
(2)公司制定产品加工方案如下:可由每个厂家单独完成,也可由两个厂共同合作完成.在加工过程中,公司需派一名工程师每天到厂家进行技术指导,并负担每天的补助费5元.请你帮公司选择一种既省钱又省时的加工方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在数轴上点A、B、C表示的数分别为﹣2,1,6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.

(1)则AB= ,BC= ,AC= ;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:BC﹣AB的值是否随着运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值;
(3)由第(1)小题可以发现,AB+BC=AC.若点C以每秒3个单位长度的速度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动.请问:随着运动时间t的变化,AB、BC、AC之间是否存在类似于(1)的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数
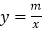 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式
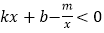 的解集(请直接写出答案).
的解集(请直接写出答案).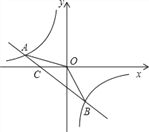
相关试题

