【题目】已知:如图一次函数y= ![]() x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y= ![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y= ![]() x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
参考答案:
【答案】
(1)
解:将B(0,1),D(1,0)的坐标代入y= ![]() x2+bx+c,
x2+bx+c,
得: 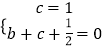 ,
,
得解析式y= ![]() x2﹣
x2﹣ ![]() x+1
x+1
(2)
解:设C(x0,y0)(x0≠0,y0≠0),
则有 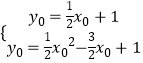 解得
解得 ![]() ,
,
∴C(4,3)
由图可知:S四边形BDEC=S△ACE﹣S△ABD,又由对称轴为x= ![]() 可知E(2,0),
可知E(2,0),
∴S= ![]() AEy0﹣
AEy0﹣ ![]() AD×OB=
AD×OB= ![]() ×4×3﹣
×4×3﹣ ![]() ×3×1=
×3×1= ![]()
(3)
解:设符合条件的点P存在,令P(a,0):
当P为直角顶点时,如图:过C作CF⊥x轴于F;
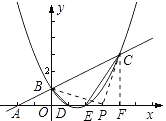
∵∠BPO+∠OBP=90°,∠BPO+∠CPF=90°,
∴∠OBP=∠FPC,
∴Rt△BOP∽Rt△PFC,
∴ ![]() ,
,
即 ![]() ,
,
整理得a2﹣4a+3=0,
解得a=1或a=3;
∴所求的点P的坐标为(1,0)或(3,0),
综上所述:满足条件的点P共有2个.
【解析】(1)根据直线BC的解析式,可求得点B的坐标,由于B、D都在抛物线的图象上,那么它们都满足该抛物线的解析式,通过联立方程组即可求得待定系数的值.(2)根据抛物线的解析式,可求得E点的坐标,联立直线BC的解析式,可求得C点坐标;那么四边形BDEC的面积即可由△AEC、△ABD的面积差求得.(3)假设存在符合条件的P点,连接BP、CP,过C作CF⊥x轴于F,若∠BPC=90°,则△BPO∽△CPF,可设出点P的坐标,分别表示出OP、PF的长,根据相似三角形所得比例线段即可求得点P的坐标.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将1,
 ,
,  ,
,  按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块三角板的直角顶点重合.
(1)写出以点C为顶点的相等的角;
(2)若∠ACB=150°,求∠DCE的度数;
(3)写出∠ACB与∠DCE之间所具有的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4 cm,AD=12 cm,点P在AD边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,当运动时间=_____时线段PQ∥AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区调查社区居民双休日的学习状况,采取下列调查方式:①从一幢高层住宅楼中选取200名居民;②从不同住层楼中随机选取200名居民;③选取社区内的200名在校学生.

(1)上述调查方式最合理的是 (填序号);
(2)将最合理的调查方式得到的数据制成扇形统计图(如图①)和频数分布直方图(如图②).
①请补全直方图(直接画在图②中);
②在这次调查中,200名居民中,在家学习的有 人;
(3)请估计该社区2000名居民中双休日学习时间不少于
 的人数.
的人数. -
科目: 来源: 题型:
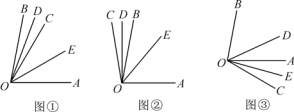
查看答案和解析>>【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
相关试题

