【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F. 
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.
参考答案:
【答案】
(1)证明:∵∠AEF=90°,
∴∠FEC+∠AEB=90°;
在Rt△ABE中,∠AEB+∠BAE=90°,
∴∠BAE=∠FEC
(2)证明:∵G,E分别是正方形ABCD的边AB,BC的中点,
∴AG=GB=BE=EC,且∠AGE=180°﹣45°=135°;
又∵CF是∠DCH的平分线,
∴∠DCF=∠FCH=45°,
∠ECF=90°+45°=135°;
在△AGE和△ECF中, 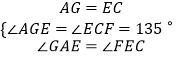 ;
;
∴△AGE≌△ECF;
(3)解:由△AGE≌△ECF,得AE=EF;
又∵∠AEF=90°,
∴△AEF是等腰直角三角形;
∵AB=a,E为BC中点,
∴BE= ![]() BC=
BC= ![]() AB=
AB= ![]() a,
a,
根据勾股定理得:AE= ![]() =
= ![]() a,
a,
∴S△AEF= ![]() a2.
a2.
【解析】(1)由于∠AEF是直角,则∠BAE和∠FEC同为∠AEB的余角,由此得证;(2)根据正方形的性质,易证得AG=EC,∠AGE=∠ECF=135°;再加(1)得出的相等角,可由ASA判定两个三角形全等;(3)在Rt△ABE中,根据勾股定理易求得AE2;由(2)的全等三角形知:AE=EF,即△AEF是等腰Rt△,因此其面积为AE2的一半,由此得解.
-
科目: 来源: 题型:
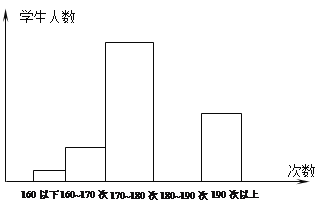
查看答案和解析>>【题目】为了解中学生的体能情况,某校抽取了50名八年级学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频数分布直方图如下图所示已知图中从左到右前第一、第二、第三、第五小组的频率分别为0.04 , 0.12 ,0.4 ,O.28 ,根据已知条件解答下列问题:
(1)第四个小组的频率是多少? 你是怎样得到的?
(2)这五小组的频数各是多少?
(3)在这次跳绳中,跳绳次数的中位数落在第几小组内?
(4)将频数分布直方图补全,并分别写出各个小组的频数,并画出频数分布折线图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并计算:已知线段AB=2 cm,延长线段AB至点C,使得2BC=AB,再反向延长AC至点D,使得AD=AC.
(1)准确地画出图形,并标出相应的字母;
(2)线段DC的中点是哪个?线段AB的长是线段DC长的几分之几?
(3)求出线段BD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将1,
 ,
,  ,
,  按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块三角板的直角顶点重合.
(1)写出以点C为顶点的相等的角;
(2)若∠ACB=150°,求∠DCE的度数;
(3)写出∠ACB与∠DCE之间所具有的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一次函数y=
 x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=  x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=  x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4 cm,AD=12 cm,点P在AD边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,当运动时间=_____时线段PQ∥AB.

相关试题

