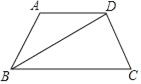
【题目】如图,四边形ABCD中,AD∥BC,∠A=120°,BD平分∠ABC.
(1)若BD⊥CD,求∠C的度数;
(2)射线AP从AB位置开始,以每秒10°的速度绕点A逆时针旋转,6秒后AP与BD有何种位置关系?并说明理由.
(3)在(2)的条件下,AP旋转一圈回到AB处时停止运动,若射线AP与直线BD相交所成的角中较小的角为x°,当10<x<20,则旋转时间t(单位:秒)的取值范围是 .
参考答案:
【答案】(1)∠C=60°;(2)PA⊥BD,理由见解析;(3)13<t <14.
【解析】
(1)在Rt△BDC中,求出∠DBC即可;
(2)结论:PA⊥BD.如图2中,设AP交BD于H.只要证明∠AHB=90°即可;
(3)如图3中,①当∠APD=20°时,易知∠DAP=30°﹣20°=10°,推出∠BAP=130°,此时t=13秒.②当∠AP′D=10°时,易知∠DAP′=30°﹣10°=20°,推出∠BAP=140°,此时t=14秒,由此即可判断.
解:(1)如图1中,
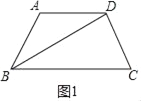
∵AD∥BC,BD平分∠ABC,
∴∠ADB=∠DBC=∠ABD,
∵∠A=120°,
∴∠ABD=∠ADB=∠DBC=30°,
∵BD⊥CD,
∴∠BDC=90°,
∴∠C=90°﹣∠DBC=60°;
(2)结论:PA⊥BD.
理由:如图2中,设AP交BD于H.
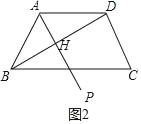
由题意∠BAP=6×10°=60°,
∵∠ABD=30°,
∴∠BAP+∠ABD=90°,
∴∠AHB=90°,
∴AP⊥BD.
(3)如图3中,
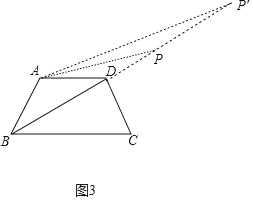
①当∠APD=20°时,易知∠DAP=30°﹣20°=10°,
∴∠BAP=130°,
此时t=13秒.
②当∠AP′D=10°时,易知∠DAP′=30°﹣10°=20°,
∴∠BAP=140°,
此时t=14秒,
∴当13<t<14时,10<x<20.
故答案为:(1)∠C=60°;(2)PA⊥BD,理由见解析;(3)13<t <14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用两个边长为15
 的小正方形拼成一个大的正方形,
的小正方形拼成一个大的正方形,(1)求大正方形的边长?
(2)若沿此大正方形边的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为720cm2?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(小方格的边长为
 ,这是某市部分简图.
,这是某市部分简图.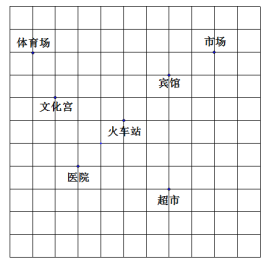
(1)请你根据下列条件建立平面直角坐标系(在图中直接画出):
①火车站为原点;
②宾馆的坐标为
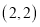 .
.(2)市场、超市的坐标分别为 、 ;
(3)请将体育场、宾馆和火车站看作三点,用线段连起来,得
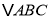 ,然后将此三角形向下平移
,然后将此三角形向下平移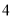 个单位长度,再画出平移后的
个单位长度,再画出平移后的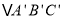 (在图中直接画出);
(在图中直接画出);(4)根据坐标情况,求
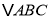 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4
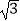 与x轴、y轴分别交于A,B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A,B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )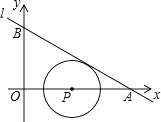
A.6
B.8
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2017﹣
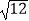 +3tan30°+|﹣
+3tan30°+|﹣ 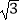 |
| -
科目: 来源: 题型:
查看答案和解析>>【题目】小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
-
科目: 来源: 题型:
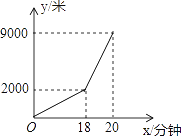
查看答案和解析>>【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
相关试题

