搜索
【题目】某公司招聘一名部门经理，对A、B、C三位候选人进行了三项测试，包括语言表达、微机操作、商品知识，各项成绩的权重分别是3，3，4，三人的成绩如下表：
候选人 | 语言表达 | 微机操作 | 商品知识 |
A | 60 | 80 | 70 |
B | 50 | 70 | 80 |
C | 60 | 80 | 65 |
请你通过计算分析一下谁会被录取？若想要B被录取，如何设计各种成绩的权重？
参考答案：
【答案】A会被录取；若想要B被录取，语言表达、微机操作、商品知识，各项成绩的权重分别是2，2，6 即可.
【解析】
运用加权平均数的计算公式：
（其中w1、w2、……、wn分别为x1、x2、……、xn的权），分别求出A、B、C三名侯选人的最终得分，即可得出结论.
∵A的平均数数 
=70， B的平均数是： 
=68，
C的平均数是： 
=68，
∴A成绩最好，A会被录取．
若想要B被录取，由于B的商品知识得分高，所以语言表达、微机操作、商品知识，各项成绩的权重分别是2，2，6 即可.
-
科目： 来源： 题型：
查看答案和解析>>【题目】课题学习：设计概率模拟实验． 在学习概率时，老师说：“掷一枚质地均匀的硬币，大量重复实验后，正面朝上的概率约是
．”小海、小东、小英分别设计了下列三个模拟实验：
小海找来一个啤酒瓶盖（如图1）进行大量重复抛掷，然后计算瓶盖口朝上的次数与总次数的比值；
小东用硬纸片做了一个圆形转盘，转盘上分成8个大小一样的扇形区域，并依次标上1至8个数字（如图2），转动转盘10次，然后计算指针落在奇数区域的次数与总次数的比值；
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子（如图3），其中有三枚是白子，一枚是黑子，从中随机同时摸出两枚棋子，并大量重复上述实验，然后计算摸出的两枚棋子颜色不同的次数与总次数的比值．
根据以上材料回答问题：
小海、小东、小英三人中，哪一位同学的实验设计比较合理，并简要说出其他两位同学实验的不足之处． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲乙两支篮球队进行了5场比赛，比赛成绩绘制成了统计图（如图）
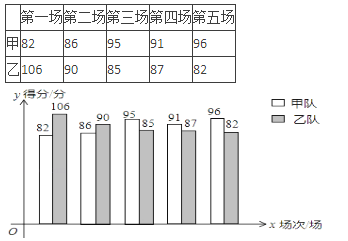
（1）分别计算甲乙两队5场比赛成绩的平均分．
（2）就这5场比赛，分别计算两队成绩的极差；
（3）就这5场比赛，分别计算两队成绩的方差；
（4）如果从两队中选派一支球队参加篮球锦标赛，根据上述统计，从平均分、极差、方差以及获胜场数这四个方面分别进行简要分析，你认为选派哪支球队参赛更能取得好成绩？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．
（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．
（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠ABC=90°，DE⊥AC于点E，且AE=CE，DE=5，EB=12．
（1）求AD的长；
（2）若∠CAB=30°，求四边形ABCD的周长． -
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程指：含有一个未知数，且未知数的最高次数为2的等式，求一元二次方程
解的方法如下：第一步：先将等式左边关于x的项进行配方， 
，第二步：配出的平方式保留在等式左边，其余部分移到等式右边，
；第三步：根据平方的逆运算，求出
或-3；第四步：求出
.类比上述求一元二次方程根的方法，（1）解一元二次方程：
；（2）求代数式
的最小值； -
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读下面例题的解法，然后解答问题：
例：若多项式2x3-x2+m分解因式的结果中有因式2x+1，求实数m的值.
解：设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0，则2x+1=0或A=0.
由2x+1=0，解得x=-
.∴x=-
是方程2x3-x2+m=0的解.∴2×(-
)3-(-)2+m=0，即-
-+m=0.∴m=
.请你模仿上面的方法尝试解决下面的问题：
若多项式x4+mx3+nx-16分解因式的结果中有因式(x-1)和(x-2)，求实数m，n的值.
相关试题
