【题目】如图,在四边形ABCD中,∠ABC=90°,DE⊥AC于点E,且AE=CE,DE=5,EB=12. 
(1)求AD的长;
(2)若∠CAB=30°,求四边形ABCD的周长.
参考答案:
【答案】
(1)解:∵∠ABC=90°,AE=CE,EB=12,
∴EB=AE=CE=12.
∵DE⊥AC,DE=5,
∴在Rt△ADE中,
由勾股定理得AD= ![]() =
= ![]() =13
=13
(2)解:∵在Rt△ABC中,∠CAB=30°,AC=AE+CE=24,
∴BC=12,AB=ACcos30°=12 ![]() ,
,
∵DE⊥AC,AE=CE,
∴AD=DC=13,
∴四边形ABCD的周长为AB+BC+CD+AD=38+12 ![]()
【解析】(1)根据等腰三角形的性质和勾股定理即可得到结论;(2)解直角三角形求出各边的长,于是得到结论.
【考点精析】利用勾股定理的概念和解直角三角形对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
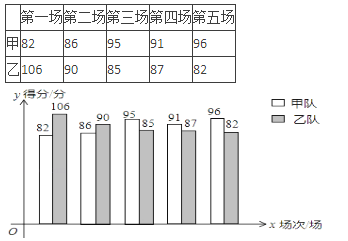
(1)分别计算甲乙两队5场比赛成绩的平均分.
(2)就这5场比赛,分别计算两队成绩的极差;
(3)就这5场比赛,分别计算两队成绩的方差;
(4)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、极差、方差以及获胜场数这四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘一名部门经理,对A、B、C三位候选人进行了三项测试,包括语言表达、微机操作、商品知识,各项成绩的权重分别是3,3,4,三人的成绩如下表:
候选人
语言表达
微机操作
商品知识
A
60
80
70
B
50
70
80
C
60
80
65
请你通过计算分析一下谁会被录取?若想要B被录取,如何设计各种成绩的权重?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程指:含有一个未知数,且未知数的最高次数为2的等式,求一元二次方程
 解的方法如下:第一步:先将等式左边关于x的项进行配方,
解的方法如下:第一步:先将等式左边关于x的项进行配方,  ,第二步:配出的平方式保留在等式左边,其余部分移到等式右边,
,第二步:配出的平方式保留在等式左边,其余部分移到等式右边, ;第三步:根据平方的逆运算,求出
;第三步:根据平方的逆运算,求出 或-3;第四步:求出
或-3;第四步:求出 .类比上述求一元二次方程根的方法,(1)解一元二次方程:
.类比上述求一元二次方程根的方法,(1)解一元二次方程: ;
;(2)求代数式
 的最小值;
的最小值; -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面例题的解法,然后解答问题:
例:若多项式2x3-x2+m分解因式的结果中有因式2x+1,求实数m的值.
解:设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0,则2x+1=0或A=0.
由2x+1=0,解得x=-
 .
.∴x=-
 是方程2x3-x2+m=0的解.
是方程2x3-x2+m=0的解.∴2×(-
 )3-(-
)3-(- )2+m=0,即-
)2+m=0,即- -
- +m=0.
+m=0.∴m=
 .
.请你模仿上面的方法尝试解决下面的问题:
若多项式x4+mx3+nx-16分解因式的结果中有因式(x-1)和(x-2),求实数m,n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射手在相同条件下打靶,射中的环数如图所示,利用图中提供的信息,解答下列问题:
(1)分别求甲、乙两名射手中环数的众数和平均数;
(2)如果从甲、乙两名射手中选一名去参加射击比赛,你选谁去?为什么?

相关试题

