【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,若∠ABC=30°,∠C=45°,ED=![]() ,点H是BD上的一个动点,则HG+HC的最小值为______________.
,点H是BD上的一个动点,则HG+HC的最小值为______________.

参考答案:
【答案】![]()
【解析】
首先证明四边形BEDG是菱形,作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在Rt△EMC中,求出EM、MC即可解决问题.
解:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
∴△EFD≌△GFB(AAS)
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
如图,作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小
在Rt△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2![]()
![]() ,
,
∴EM=![]() BE=
BE=![]() ,
,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=![]() ,MN=DE=2
,MN=DE=2![]() ,
,
在Rt△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=![]() ,
,
∴MC=3![]() ,
,
在Rt△EMC中,∵∠EMC=90°,EM=![]() .MC=3
.MC=3![]() ,
,
∴EC=![]() =5
=5![]() .
.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为5![]() .
.
故答案为5![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.

(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F=
 ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;(3)求证:GF2﹣GB2=DFGF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线l1:y=﹣x2+bx+3交x轴于点A、B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣5).
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA、PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴(如图2所示),交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
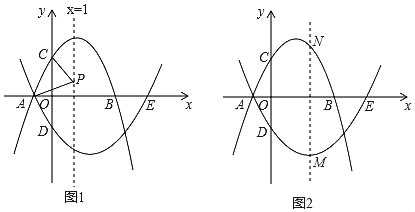
-
科目: 来源: 题型:
查看答案和解析>>【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“
 ”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如将多项式
”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如将多项式 因式分解的结果为
因式分解的结果为 ,当
,当 时,
时, ,
, ,
, ,此时可以得到数字密码
,此时可以得到数字密码 或
或 等.
等.(1)根据上述方法,当
 ,
, 时,对于多项式
时,对于多项式 分解因式后可以形成哪些数字密码(写出四个即可)?
分解因式后可以形成哪些数字密码(写出四个即可)?(2)将多项式
 因式分解成三个一次式的乘积后,利用题目中所示的方法,当
因式分解成三个一次式的乘积后,利用题目中所示的方法,当 时可以得到密码
时可以得到密码 ,求
,求 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰
 中,
中, 是BC边上的高,且
是BC边上的高,且 ,则等腰
,则等腰 底角的度数为__________.
底角的度数为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若B(﹣
 ,y1),C(﹣
,y1),C(﹣ ,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④
,y2)为图象上的两点,则y1<y2;③2a﹣b=0;④ <0,其中正确的结论是_____.
<0,其中正确的结论是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位运动员在相同条件下各射靶
 次,每次射靶的成绩如下:
次,每次射靶的成绩如下:甲:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
乙:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
丙:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
(1)根据以上数据完成下表:
平均数
中位数
方差
甲


__________
乙
__________


丙

__________

(2)根据表中数据分析,哪位运动员的成绩最稳定.并简要说明理由.
相关试题

