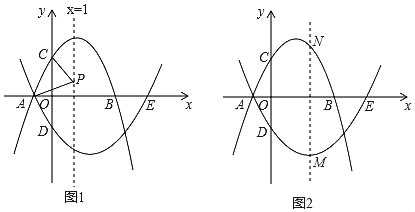
【题目】如图1，抛物线l1：y=﹣x2+bx+3交x轴于点A、B，（点A在点B的左侧），交y轴于点C，其对称轴为x=1，抛物线l2经过点A，与x轴的另一个交点为E（5，0），交y轴于点D（0，﹣5）．

（1）求抛物线l2的函数表达式；

（2）P为直线x=1上一动点，连接PA、PC，当PA=PC时，求点P的坐标；

（3）M为抛物线l2上一动点，过点M作直线MN∥y轴（如图2所示），交抛物线l1于点N，求点M自点A运动至点E的过程中，线段MN长度的最大值．

参考答案：

【答案】（1）抛物线l2的函数表达式；y=x2﹣4x﹣5；（2）P点坐标为（1，1）；（3）在点M自点A运动至点E的过程中，线段MN长度的最大值为12.5．

【解析】

（1）由抛物线l1的对称轴求出b的值，即可得出抛物线l1的解析式，从而得出点A、点B的坐标，由点B、点E、点D的坐标求出抛物线l2的解析式即可；（2）作CH⊥PG交直线PG于点H，设点P的坐标为（1，y），求出点C的坐标，进而得出CH=1，PH=|3﹣y |，PG=|y |，AG=2，由PA=PC可得PA2=PC2，由勾股定理分别将PA2、PC2用CH、PH、PG、AG表示，列方程求出y的值即可；（3）设出点M的坐标，求出两个抛物线交点的横坐标分别为﹣1，4，①当﹣1＜x≤4时，点M位于点N的下方，表示出MN的长度为关于x的二次函数，在x的范围内求二次函数的最值；②当4＜x≤5时，点M位于点N的上方，同理求出此时MN的最大值，取二者较大值，即可得出MN的最大值.

（1）∵抛物线l1：y=﹣x2+bx+3对称轴为x=1，

∴x=﹣=1，b=2，

∴抛物线l1的函数表达式为：y=﹣x2+2x+3，

当y=0时，﹣x2+2x+3=0，

解得：x1=3，x2=﹣1，

∴A（﹣1，0），B（3，0），

设抛物线l2的函数表达式；y=a（x﹣5）（x+1），

把D（0，﹣5）代入得：﹣5a=﹣5，a=1，

∴抛物线l2的函数表达式；y=x2﹣4x﹣5；

（2）作CH⊥PG交直线PG于点H，

设P点坐标为（1，y），由（1）可得C点坐标为（0，3），

∴CH=1，PH=|3﹣y |，PG=|y |，AG=2，

∴PC2=12+（3﹣y）2=y2﹣6y+10，PA2= =y2+4，

∵PC=PA，

∴PA2=PC2，

∴y2﹣6y+10=y2+4，解得y=1，

∴P点坐标为（1，1）；

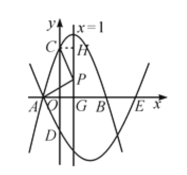
（3）由题意可设M（x，x2﹣4x﹣5），

∵MN∥y轴，

∴N（x，﹣x2+2x+3），

令﹣x2+2x+3=x2﹣4x﹣5，可解得x=﹣1或x=4，

①当﹣1＜x≤4时，MN=（﹣x2+2x+3）﹣（x2﹣4x﹣5）=﹣2x2+6x+8=﹣2（x﹣）2+，

显然﹣1＜≤4，

∴当x=时，MN有最大值12.5；

②当4＜x≤5时，MN=（x2﹣4x﹣5）﹣（﹣x2+2x+3）=2x2﹣6x﹣8=2（x﹣）2﹣，

显然当x＞时，MN随x的增大而增大，

∴当x=5时，MN有最大值，MN=2（5﹣）2﹣=12.

综上可知：在点M自点A运动至点E的过程中，线段MN长度的最大值为12.5．

关闭