【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:

①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
参考答案:
【答案】③.
【解析】试题分析:首先利用对角线互相平分的四边形是平行四边形判定该四边形为平行四边形,然后结合菱形的判定得到答案即可.
解:由题意得:BD=CD,ED=FD,
∴四边形EBFC是平行四边形,
①BE⊥EC,根据这个条件只能得出四边形EBFC是矩形,
②BF∥CE,根据EBFC是平行四边形已可以得出BF∥CE,因此不能根据此条件得出菱形,
③AB=AC,
∵![]() ,
,
∴△ADB≌△ADC,
∴∠BAD=∠CAD
∴△AEB≌△AEC(SAS),
∴BE=CE,
∴四边形BECF是菱形.
故答案为:③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为2、5,则三角形的周长为______.
-
科目: 来源: 题型:
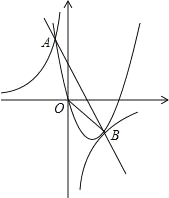
查看答案和解析>>【题目】如图,直线y=-2x+2与抛物线y=ax2+bx(a<0)相交于点A,B.双曲线y=
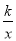 过A、B两点,已知点B的坐标为(2,-2),点A在第二象限内,且tan∠Aoy=
过A、B两点,已知点B的坐标为(2,-2),点A在第二象限内,且tan∠Aoy=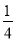 .
.
(1)求双曲线和抛物线的解析式;
(2)计算△AOB的面积;
(3)在抛物线上是否存在点P,使△AOP的面积等于△AOB的面积?若存在,请你写出点P的坐标;若不存在,请你说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
求:
(1)转动转盘,转出的数字大于3的概率是多少;
(2)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式中,结果等于a6 的是( )
A. a4+a2 B. a2+a2+a2 C. a2·a2·a2 D. a3·a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个n边形的每个内角为144°,则这个是正( )边形。
A. 五B. 七C. 九D. 十
-
科目: 来源: 题型:
查看答案和解析>>【题目】一般地,n个相同的因数a相乘(即) a×a×a … a记 为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)请探究log24、log216、log264之间的数量关系_______ 。
相关试题

