Question

【题目】如图，直线y=-2x+2与抛物线y=ax2+bx（a＜0）相交于点A，B．双曲线y=过A、B两点，已知点B的坐标为（2，-2），点A在第二象限内，且tan∠Aoy=．

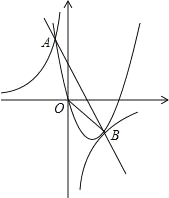
（1）求双曲线和抛物线的解析式；

（2）计算△AOB的面积；

（3）在抛物线上是否存在点P，使△AOP的面积等于△AOB的面积？若存在，请你写出点P的坐标；若不存在，请你说明理由．

Answer 1

【答案】（1）双曲线解析式为y=-，抛物线解析式为y=x2-3x，（2）3，（3）P（-3，18）．

【解析】

试题分析：（1）先用待定系数法求出双曲线解析式，再用待定系数法求出抛物线解析式；

（2）先求出△AOB的面积，在求出△BOC的面积即可；

（3）先求出直线PB解析式为y=-4x+6，和抛物线解析式为y=x2-3x，联立方程组求解即可．

试题解析：（1）∵双曲线经过点B，

∴k=-4，

∴双曲线解析式为y=-，

∵tan∠AOy=，

设A（-m，4m），

∵点A 过双曲线，

∴m=1或m=-1（舍），

∴A（-1，4）；

∵抛物线过点A，B，

∴，

∴，

∴抛物线解析式为y=x2-3x，

（2）设直线y=-2x+2交于x轴于C，令y=0，

∴x=1，

∴OC=1，

∴S△AOB=S△AOC+S△BOC=×1×4+×1×2=3，

（3）存在点P（-3，18），

理由：假设存在点P，使△AOP的面积等于△AOB的面积；

∴点P到直线OA的距离等于点B到直线OA的距离，

∴PB∥AO，

∵直线AO解析式为y=-4x，

∴设直线PB的解析式为y=-4x+f，

∵直线PB过点B，

∴-2=-4×2+f，

∴f=6，

∴直线PB解析式为y=-4x+6，

∴，

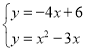∴或（舍），

P（-3，18）．