【题目】附加题:如图,已知在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上由B点向C点运动,同时,点Q在线段CA上由点C向点A运动. 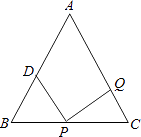
(1)如果点P、Q的速度均为3厘米/秒,经过1秒后,△BPD与△CQP是否全等?请说明理由;
(2)若点P的运动速度为2厘米/秒,点Q的运动速度为2.5厘米/秒,是否存在某一个时刻,使得△BPD与△CQP全等?如果存在请求出这一时刻并证明;如果不存在,请说明理由.
参考答案:
【答案】
(1)解:△BPD与△CQP是全等,
理由是:当t=1秒时BP=CQ=3,
CP=8﹣3=5,
∵D为AB中点,
∴BD= ![]() AC=5=CP,
AC=5=CP,
∵AB=AC,
∴∠B=∠C,
在△BDP和△CPQ中
∵ 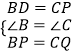 ,
,
∴△BDP≌△CPQ(SAS)
(2)解:假设存在时间t秒,使△BDP和△CPQ全等,
则BP=2t,BD=5,CP=8﹣2t,CQ=2.5t,
∵△BDP和△CPQ全等,∠B=∠C,
∴ ![]() 或
或 ![]() (此方程组无解),
(此方程组无解),
解得:t=2,
∴存在时刻t=2秒时,△BDP和△CPQ全等,
此时BP=4,BD=5,CP=8﹣4=4=BP,CQ=5=BD,
在△BDP和△CQP中
∵  ,
,
∴△BDP≌△CQP(SAS).
【解析】(1)求出BP=CQ,CP=BD,∠B=∠C,根据SAS证出两三角形全等即可;(2)假设存在时刻t,根据全等三角形的性质得出方程组,求出t后,看看是否符合题意,再根据全等三角形的判定推出即可.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图,现将△ABC平移后得△EDF,使点B的对应点为点D,点A对应点为点E.

(1)画出△EDF;
(2)线段BD与AE有何关系?
(3)连接CD、BD,则四边形ABDC的面积为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC.
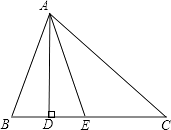
(1)已知∠B=60°,∠B=30°,求∠DAE的度数;
(2)已知∠B=3∠C,说明:∠DAE=∠C. -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线 y=﹣2x2 向左平移 3 个单位,再向下平移 4 个单位,所得抛物线为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程中,两根之和为1的是( )
A. x2+x+1=0B. x2﹣x+3=0C. 2x2﹣x﹣1=0D. x2﹣x﹣5=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】以
 为自变量的二次函数
为自变量的二次函数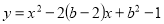 的图象不经过第三象限,则实数
的图象不经过第三象限,则实数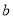 的取值范围是
的取值范围是A.
 B.
B.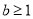 或
或 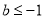 C.
C.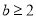 D.
D. 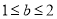
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式两边同时乘以一个整数,不等号方向不变。()
相关试题

