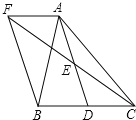
【题目】如图,在![]() 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且![]() ,连接BF.
,连接BF.
![]() 证明:
证明:![]() ;
;
![]() 当
当![]() 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.
参考答案:
【答案】见解析
【解析】试题分析:
(1)由已知易证△AEF≌△DEC,由此可得CD=AF结合AF=BD,即可得到BD=CD;
(2)由AF=BD,AF∥BC易得四边形AFBD是平行四边形,因此只需添加条件AB=AC,结合BD=CD即可得到∠ADB=90°,从而可得此时四边形AFBD是矩形.
试题解析:
(1)∵AF∥BC,点E是AD的中点,
∴∠AFE=∠DCE,AE=DE,
又∵∠AEF=∠DEC,
∴△AEF≌△DEC,
∴AF=CD,
又∵AF=BD,
∴BD=CD;
(2)在△ABC中,当AB=AC时,四边形AFBD是矩形,理由如下:
∵AF∥BC,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴∠ADB=90°,
∴平行四边形AFBD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, 分别平分
分别平分 的外角
的外角 、内角
、内角 、外角
、外角 .以下结论:①
.以下结论:① ;②
;② ;③
;③ 平分
平分 ;④
;④ ;⑤
;⑤ .其中正确的结论有( ).
.其中正确的结论有( ).
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校标准化建设需购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑和每台电子白板各多少万元;
(2)根据学校需要,实际购进电脑和电子白板共30台,总费用30万元,请你通过计算求学校购买了电脑和电子白板各多少台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数的图象过点
 ,且顶点坐标为
,且顶点坐标为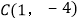 .
.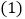 求此二次函数的表达式;
求此二次函数的表达式;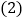 画出此函数图象,并根据函数图象写出:当
画出此函数图象,并根据函数图象写出:当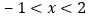 时,y的取值范围.
时,y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶
小瓶
进价(元/瓶)
5
2
售价(元/瓶)
7
3
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,∠MON =70°,点A、B在∠MON的两条边上运动,∠MAB与∠NBA的平分线交于点P.
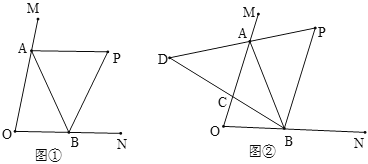
(1)点A、B在运动过程中,∠P的大小会变吗?若不会,求∠P的度数;若会,请说明理由.
(2)如图②,继续作BC平分∠ABO,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?若不会,求出∠D的度数;若会,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:
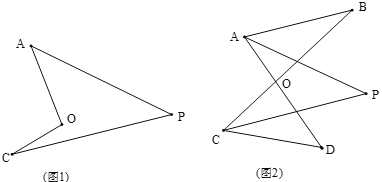
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,∠AOC与∠A、∠C、∠P的数量关系为_______.
(2)如图(2),已知AP平分∠BAD,CP平分∠BCD,∠B =28°,∠D=48°.求∠P的度数.
由(1)结论得:∠AOC =∠PAO +∠PCO+∠P
所以2∠AOC=2∠PAO +2∠PCO+2∠P即2∠AOC =∠BAO +∠DCO+2∠P
因为∠AOC =∠BAO +∠B,∠AOC =∠DCO +∠D
所以2∠AOC=∠BAO +∠DCO+∠B +∠D
所以∠P=_______.
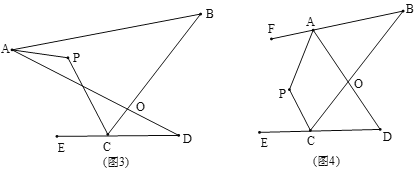
解决问题:
(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______;
(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是_______.
相关试题

