【题目】如图,![]() ,
,![]() 分别平分
分别平分![]() 的外角
的外角![]() 、内角
、内角![]() 、外角
、外角![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的结论有( ).
.其中正确的结论有( ).

A.1个B.2个C.3个D.4个
参考答案:
【答案】D
【解析】
根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EAC=∠ABC+∠ACB=2∠ABC,根据角平分线的定义可得∠EAC=2∠EAD,然后求出∠EAD=∠ABC,再根据同位角相等,两直线平行可得AD∥BC,判断出①正确;
根据两直线平行,内错角相等可得∠ADB=∠CBD,再根据角平分线的定义可得∠ABC=2∠CBD,从而得到∠ACB=2∠ADB,判断出②正确;
根据两直线平行,内错角相等可得∠ADC=∠DCF,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义整理可得∠ADC=90°-∠ABD,判断出④正确;
根据三角形的外角性质与角平分线的定义表示出∠DCF,然后整理得到∠BDC=![]() ∠BAC,判断出⑤正确;再根据两直线平行,内错角相等可得∠CBD=∠ADB,∠ABC与∠BAC不一定相等,所以∠ADB与∠BDC不一定相等,判断出③错误.
∠BAC,判断出⑤正确;再根据两直线平行,内错角相等可得∠CBD=∠ADB,∠ABC与∠BAC不一定相等,所以∠ADB与∠BDC不一定相等,判断出③错误.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
∵AD∥BC,
∴∠ADC=∠DCF,
∵CD是∠ACF的平分线,
∴∠ADC=![]() ∠ACF=
∠ACF=![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)=![]() (180°-∠ACB)=
(180°-∠ACB)=![]() (180°-∠ABC)=90°-∠ABD,
(180°-∠ABC)=90°-∠ABD,
∴④正确;
∵∠BDC=∠DCF-∠DBF=![]() ∠ACF-
∠ACF-![]() ∠ABC=
∠ABC=![]() ∠BAC,
∠BAC,
∴⑤正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC=![]() ∠ABC,
∠ABC,
∵∠ADB=∠DBC=![]() ∠ABC,∠BDC=
∠ABC,∠BDC=![]() ∠BAC,
∠BAC,
∵∠ABC与∠BAC不一定相等,
∴∠ADB与∠BDC不一定相等,
∴③错误.
综上所述,结论正确的是①②④⑤共4个.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各句判定矩形的说法
 对角线相等的四边形是矩形;
对角线相等的四边形是矩形; 对角线互相平分且相等的四边形是矩形;
对角线互相平分且相等的四边形是矩形; 有一个角是直角的四边形是矩形;
有一个角是直角的四边形是矩形; 有四个角是直角的四边形是矩形;
有四个角是直角的四边形是矩形; 四个角都相等的四边形是矩形;
四个角都相等的四边形是矩形; 对角线相等,且有一个角是直角的四边形是矩形;是正确有几个
对角线相等,且有一个角是直角的四边形是矩形;是正确有几个
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
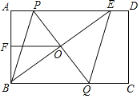
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系,并说明理由;
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通常情况下,
 不一定等于
不一定等于 ,但我们数学上存在这样一些特殊的数对,观察:
,但我们数学上存在这样一些特殊的数对,观察: ,
, ,
, ,…,我们把符合
,…,我们把符合 的两个数叫做“和积数对”,已知
的两个数叫做“和积数对”,已知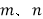
 是一对“和积数对”.
是一对“和积数对”.(1)请举出一对
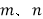 是“和积数对”,并验证其正确性;
是“和积数对”,并验证其正确性;(2)求代数式
 的值;
的值;(3)小明发现了一个关于
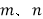 的结论:
的结论: ;你认为小明发现的结论正确吗?请说明理由.
;你认为小明发现的结论正确吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校标准化建设需购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑和每台电子白板各多少万元;
(2)根据学校需要,实际购进电脑和电子白板共30台,总费用30万元,请你通过计算求学校购买了电脑和电子白板各多少台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数的图象过点
 ,且顶点坐标为
,且顶点坐标为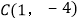 .
.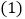 求此二次函数的表达式;
求此二次函数的表达式; 画出此函数图象,并根据函数图象写出:当
画出此函数图象,并根据函数图象写出:当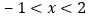 时,y的取值范围.
时,y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
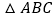 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且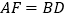 ,连接BF.
,连接BF. 证明:
证明: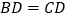 ;
; 当
当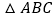 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.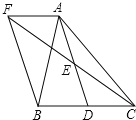
相关试题

