【题目】(1.2计算3.4分解因式)
(1)( ![]() +1)0﹣(﹣
+1)0﹣(﹣ ![]() )2+2﹣2
)2+2﹣2
(2)(2a﹣3b)(﹣3b﹣2a)
(3)3m2﹣24m+48
(4)x3y﹣4xy.
参考答案:
【答案】
(1)解:原式=1﹣ ![]() +
+ ![]() =1
=1
(2)解:(2a﹣3b)(﹣3b﹣2a)
=﹣6ab﹣4a2+9b2+6ab
=﹣4a2+9b2
(3)解:原式=3(m2﹣8m+16)=3(m﹣4)2
(4)解:原式=xy(x2﹣4)=xy(x﹣2)(x+2)
【解析】(1)直接利用零指数幂的性质以及负整数指数幂的性质化简求出答案;(2)直接利用多项式乘法计算得出答案;(3)首先提取公因式3,进而利用完全平方公式分解因式得出答案;(4)首先提取公因式x,进而利用平方差公式分解因式得出答案.
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意的整数n,能整除(n+3)(n﹣3)﹣(n+2)(n﹣2)的整数是( )
A.4
B.3
C.﹣5
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=
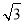 ,求图中阴影部分的面积.
,求图中阴影部分的面积.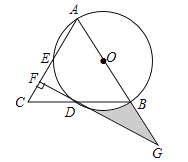
-
科目: 来源: 题型:
查看答案和解析>>【题目】某织布厂有 150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣 4 件,制衣一件需要布 1.5m,将布直接出售,每米布可获利 2 元,将布制成衣后出售,每件可获利 25 元,若每名工人只能做一项工作,且不计其他因素,设安排 x 名工人制衣.
(1)一天中制衣所获利润 元(用含 x 的式表示);
(2)一天中销售剩余的布所获利润为 元(用含 x 的式表示);
(3)一天当中安排 名工人制衣时,所获利润为 13712 元;
(4)一年按 300 天计算,一年中这个工厂所获利润最大值为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:52n=a,4n=b,则102n= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学积极组织学生开展课外阅读活动,为了解本校1500名学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)这次抽样调查的样本容量是;
(2)x= , 并将不完整的条形统计图补充完整;
(3)若满足t≥3的人数为合格,那么估计该中学每周课外阅读时间量合格人数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式bx2+2abx+a2b分解因式的结果是_____.
相关试题

