【题目】如图,矩形![]() 的顶点A、C分别在
的顶点A、C分别在![]() 、
、![]() 的正半轴上,反比例函数
的正半轴上,反比例函数![]() (
(![]() )与矩形
)与矩形![]() 的边AB、BC交于点D、E.
的边AB、BC交于点D、E.

(1)若![]() ,则
,则![]() 的面积为_________;
的面积为_________;
(2)若D为AB边中点.
①求证:E为BC边中点;
②若![]() 的面积为4,求
的面积为4,求![]() 的值.
的值.
参考答案:
【答案】(1)1;(2)①见解析;②![]()
【解析】
(1)根据题意,可设点E(a,![]() ),继而由三角形的面积公式即可求
),继而由三角形的面积公式即可求![]() 的面积;
的面积;
(2)①设![]() ,则
,则![]() ,
,![]() ,继而代入反比例函数可得x与a的关系,继而根据点B、点E的横坐标即可求证结论;
,继而代入反比例函数可得x与a的关系,继而根据点B、点E的横坐标即可求证结论;
②利用分割法求出![]() ,再将数据代入解方程即可.
,再将数据代入解方程即可.
解:(1)根据题意,可设点E(a,![]() ),
),
∴S△OCE=![]()
![]()
![]()
故![]() 的面积为1;
的面积为1;
(2)①证明:设![]() ,
,
∵![]() 为
为![]() 边中点,
边中点,
∴![]() ,
,
∵点![]() ,
,![]() 在矩形
在矩形![]() 的同一边上,
的同一边上,
∴![]() ,
,
又∵点![]() 在反比例函数图像上,
在反比例函数图像上,
∴![]() ,
,![]() ,
,
即![]() ,
,
∴![]() 为
为![]() 边中点,
边中点,
(3)![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 相交于点
相交于点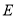 ,
, ,射线
,射线 在
在 内(如图1).
内(如图1).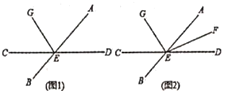
(1)若
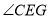 比
比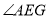 小25度,求
小25度,求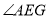 的大小;
的大小;(2)若射线
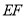 平分
平分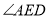 ,
,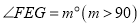 (如图2),则
(如图2),则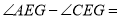 (用含
(用含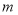 的代数式表示,请直接写出结果)
的代数式表示,请直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】疫情发生后,口罩成了人们生活的必需品.某药店销售A,B两种口罩,今年3月份的进价如下表:

(1)已知B种口罩每包售价比A种口罩贵20元,用64元购买到A种口罩的数量和144元购买到B种口罩的数量相同,求A种口罩和B种口罩每包售价.
(2)为满足不同顾客的需求,该药店准备4月份新增购进进价为每包10元的C种口罩,A种和B种口罩仍按需购进,进价与3月份相同,A种口罩的数量是B种口罩的5倍,共花费12000元,则该店至少可以购进三种口罩共多少包?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连结OD、OE、OC,对于下列结论:
①AD+BC=CD;②∠DOC=90°;③S梯形ABCD=
 CDOA;④
CDOA;④ .
. 其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于受到手机更新换代的影响,某手机店经销
 型号手机四月售价比三月每台降价500元.如果卖出相同数量的
型号手机四月售价比三月每台降价500元.如果卖出相同数量的 型号手机,那么三月销售额为9万元,四月销售额只有8万元.
型号手机,那么三月销售额为9万元,四月销售额只有8万元.(1)三月
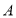 型号手机每台售价为多少元?
型号手机每台售价为多少元?(2)为了提高利润,该店计划五月购进
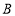 型号手机销售,已知
型号手机销售,已知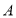 型号每台进价为3500元,
型号每台进价为3500元,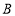 型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?(3)该店计划六月对
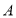 型号的尾货进行销售,决定在四月售价基础上每售出一台
型号的尾货进行销售,决定在四月售价基础上每售出一台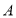 型号手机再返还顾客现金
型号手机再返还顾客现金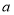 元,而
元,而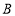 型号按销售价4400元销售,如要使(2)中所有方案获利相同,
型号按销售价4400元销售,如要使(2)中所有方案获利相同,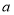 应取何值?
应取何值? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
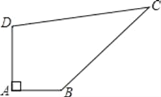
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
(1)求证:FE=FD;
(2)若∠CAD=∠CAB=24°,求∠EDF的度数
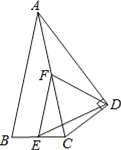
相关试题

