【题目】疫情发生后,口罩成了人们生活的必需品.某药店销售A,B两种口罩,今年3月份的进价如下表:

(1)已知B种口罩每包售价比A种口罩贵20元,用64元购买到A种口罩的数量和144元购买到B种口罩的数量相同,求A种口罩和B种口罩每包售价.
(2)为满足不同顾客的需求,该药店准备4月份新增购进进价为每包10元的C种口罩,A种和B种口罩仍按需购进,进价与3月份相同,A种口罩的数量是B种口罩的5倍,共花费12000元,则该店至少可以购进三种口罩共多少包?
参考答案:
【答案】(1)![]() 种口罩每包售价16元,
种口罩每包售价16元,![]() 种口罩每包售价36元;(2)822包
种口罩每包售价36元;(2)822包
【解析】
(1)设![]() 种口罩每包售价
种口罩每包售价![]() 元,则
元,则![]() 种口罩每包售价
种口罩每包售价![]() 元,根据等量关系:用64元购买到A种口罩的数量和144元购买到B种口罩的数量相同,列出方程并解方程即可.
元,根据等量关系:用64元购买到A种口罩的数量和144元购买到B种口罩的数量相同,列出方程并解方程即可.
(2)设![]() 种口罩买
种口罩买![]() 包,
包,![]() 种口罩买
种口罩买![]() 包,则
包,则![]() 种口罩买
种口罩买![]() 包,根据等量关系:三种口罩共花费12000元,得到
包,根据等量关系:三种口罩共花费12000元,得到![]() ,进而得出总数量关于n的函数关系式,根据一次函数的最值求解即可.
,进而得出总数量关于n的函数关系式,根据一次函数的最值求解即可.
解:(1)设![]() 种口罩每包售价
种口罩每包售价![]() 元,则
元,则![]() 种口罩每包售价
种口罩每包售价![]() 元,依题意,得:
元,依题意,得:
![]()
解得:![]()
经检验:![]() 是原方程的解
是原方程的解
∴![]() ,∴
,∴![]() (元)
(元)
答:![]() 种口罩每包售价16元,
种口罩每包售价16元,![]() 种口罩每包售价36元
种口罩每包售价36元
(2)设![]() 种口罩买
种口罩买![]() 包,
包,![]() 种口罩买
种口罩买![]() 包,则
包,则![]() 种口罩买
种口罩买![]() 包
包
则![]()
![]()
∵![]() 是5的倍数,∴
是5的倍数,∴![]()
总数量为![]()
![]()
∵![]() ,∴
,∴![]() 取最大值时,
取最大值时,![]() 值最小
值最小
又∵![]()
∴当![]() 时,总口罩最少为
时,总口罩最少为
![]() (包)
(包)
∴该店至少可以购买进三种口罩共822包.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为3厘米,点B为⊙O外一点,OB交⊙O于点A,且AB=OA,动点P从点A出发,以π厘米/秒的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为( )秒时,直线BP与⊙O相切.

A. 1 B. 5 C. 0.5或5.5 D. 1或5
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
(问题探究)
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E= ;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
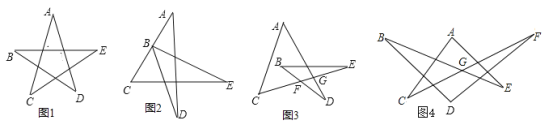
(变式拓展)
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 相交于点
相交于点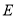 ,
, ,射线
,射线 在
在 内(如图1).
内(如图1).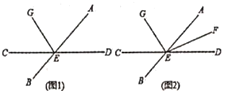
(1)若
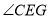 比
比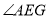 小25度,求
小25度,求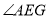 的大小;
的大小;(2)若射线
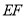 平分
平分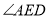 ,
,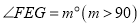 (如图2),则
(如图2),则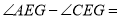 (用含
(用含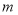 的代数式表示,请直接写出结果)
的代数式表示,请直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连结OD、OE、OC,对于下列结论:
①AD+BC=CD;②∠DOC=90°;③S梯形ABCD=
 CDOA;④
CDOA;④ .
. 其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的顶点A、C分别在
的顶点A、C分别在 、
、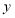 的正半轴上,反比例函数
的正半轴上,反比例函数 (
(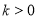 )与矩形
)与矩形 的边AB、BC交于点D、E.
的边AB、BC交于点D、E.
(1)若
 ,则
,则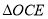 的面积为_________;
的面积为_________;(2)若D为AB边中点.
①求证:E为BC边中点;
②若
 的面积为4,求
的面积为4,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】由于受到手机更新换代的影响,某手机店经销
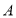 型号手机四月售价比三月每台降价500元.如果卖出相同数量的
型号手机四月售价比三月每台降价500元.如果卖出相同数量的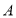 型号手机,那么三月销售额为9万元,四月销售额只有8万元.
型号手机,那么三月销售额为9万元,四月销售额只有8万元.(1)三月
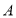 型号手机每台售价为多少元?
型号手机每台售价为多少元?(2)为了提高利润,该店计划五月购进
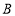 型号手机销售,已知
型号手机销售,已知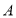 型号每台进价为3500元,
型号每台进价为3500元,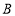 型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?(3)该店计划六月对
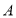 型号的尾货进行销售,决定在四月售价基础上每售出一台
型号的尾货进行销售,决定在四月售价基础上每售出一台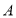 型号手机再返还顾客现金
型号手机再返还顾客现金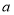 元,而
元,而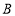 型号按销售价4400元销售,如要使(2)中所有方案获利相同,
型号按销售价4400元销售,如要使(2)中所有方案获利相同,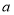 应取何值?
应取何值?
相关试题

