【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:![]() +(﹣3x2+5x﹣7)=﹣2x2+3x﹣6
+(﹣3x2+5x﹣7)=﹣2x2+3x﹣6
(1)求所捂的多项式;
(2)若x是![]() x=﹣
x=﹣![]() x+3的解,求所捂多项式的值;
x+3的解,求所捂多项式的值;
(3)若x为正整数,x每取一个值,都可以求出所捂多项式的值,请你任取x的几个值(不要写在答题纸上),发现它们之间有一定的规律,请用含x的式子表示这一结论:____________=_____________;
(4)若所捂多项式的值为729,请直接写出x的取值.
参考答案:
【答案】(1)![]() ;(2)x=4, 9;(3)
;(2)x=4, 9;(3)![]() .(4)28或-26
.(4)28或-26
【解析】
(1)根据题意列出整式相减的式子,再去括号,合并同类项即可;
(2)先求出方程的解,然后代入(1)中求得的所捂的多项式即可;
(3)令x=1,2,3,4求出所捂多项式的值,找出规律即可;
(4)根据第(3)问发现的规律进行计算即可.
解:(1)﹣2x2+3x﹣6﹣(﹣3x2+5x﹣7)=﹣2x2+3x﹣6+3x2-5x+7=x2-2x+1,
即所捂的多项式是:x22x+1;
(2)解方程![]() x=﹣
x=﹣![]() x+3,得x=4,
x+3,得x=4,
∴x22x+1=422×4+1=9,
即若x是![]() x=﹣
x=﹣![]() x+3的解,所捂多项式的值是9;
x+3的解,所捂多项式的值是9;
(3)当x=1时,x22x+1=12+1=0;
当x=2时,x22x+1=44+1=1;
当x=3时,x22x+1=96+1=4;
当x=4时,x22x+1=168+1=9,…,
由上可以发现规律是所捂多项式的值是代入的正整数x减去1所得结果的平方,
即x22x+1 =(x-1)2;
(4)若所捂多项式的值为729,则(x-1)2=729,
∴x-1=±27,
∴x的值是28或-26.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.

(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾(其中A、B、C、D分别表示可回收物、厨余垃圾、有害垃圾和其它垃圾)的分类情况,进行整理后,绘制了如下两幅尚不完整的统计图.试根据图表解答下列问题:

(1)请将图①中的条形统计图补充完整;
(2)在图②中的扇形统计图中,“D”部分所对应的圆心角等于 度;
(3)在抽样数据中,产生的有害垃圾共有多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,且a≠0,b≠0,a+b≠0,则函数y=ax+b与
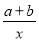 在同一坐标系中的图象不可能是( )
在同一坐标系中的图象不可能是( )A.
 B.
B. 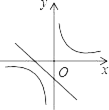
C.
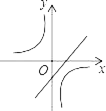 D.
D. 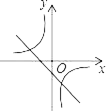
-
科目: 来源: 题型:
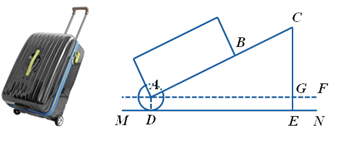
查看答案和解析>>【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆
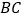 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,
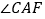 =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据: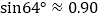 ,
,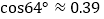 ,
,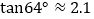 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】射阳火车站是连盐铁路(已与青连铁路合并为青盐铁路)沿线的一个县级车站,位于江苏省射阳县海河镇条海村,射阳站的建成结束了射阳县无铁路的历史。设正在行驶途中的某一时刻,记为T时刻,铁路上(双轨)迎面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD=4(单位长度),如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是b.若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,且
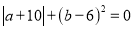 .
.(1)求此时刻快车头A与慢车头C之间相距多少单位长度?
(2)如果此时刻将数轴折叠,使点A与点C重合,则点B与数轴上表示数_____的点重合。
(3)若在T时刻,一架无人机正在B的正上方以10个单位长度/秒的速度向右匀速飞行,则问当它飞到A的正上方时,求此时AC之间的距离?
(4)从T时刻开始算起,问再行驶多少秒钟两列火车行驶到车头AC相距8个单位长度?
(5)在T时刻,快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟,他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值(即PA+PC+PB+PD为定值).你认为学生P发现的这一结论是否正确?若正确,求出这个时间及定值;若不正确,请说明理由.

相关试题

