【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾(其中A、B、C、D分别表示可回收物、厨余垃圾、有害垃圾和其它垃圾)的分类情况,进行整理后,绘制了如下两幅尚不完整的统计图.试根据图表解答下列问题:

(1)请将图①中的条形统计图补充完整;
(2)在图②中的扇形统计图中,“D”部分所对应的圆心角等于 度;
(3)在抽样数据中,产生的有害垃圾共有多少吨?
参考答案:
【答案】(1)补全统计图如图所示:见解析;(2)36;(3)在抽样数据中,产生的有害垃圾共有3吨.
【解析】
(1)根据D所占扇形统计图的百分数,和在条形图中的具体数量,计算出总量,然后与B类在扇形统计图中的百分数相乘得出数据,补全条形图即可.
(2)根据D所占扇形统计图的百分数与360°相乘即可得出相应圆心角的度数.
(3)根据A、B、D三类的百分数,算出C的百分数,然后与垃圾总量50吨相乘即可得出结果.
(1)5÷10%=50(吨),50×30%=15(吨),补全统计图如图所示:

(2)360°×10%=36°,
故答案为:36.
(3)C有害垃圾为:50×(1﹣30%﹣54%﹣10%)=3(吨)
答:在抽样数据中,产生的有害垃圾共有3吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形ABCD中,点E、F、G分别是边AD、AB、BC的中点,连接EP、FG.
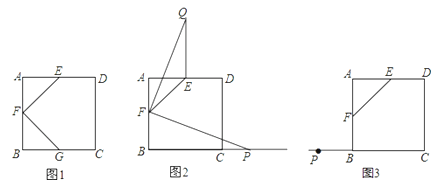
(1)如图1,直接写出EF与FG的关系____________;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FH,连接EH.
①求证:△FFE≌△PFG;②直接写出EF、EH、BP三者之间的关系;
(3)如图3,若点P为CB延长线上的一动点,连接FP,按照(2)中的做法,在图(3)中补全图形,并直接写出EF、EH、BP三者之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点E、F、G、H分别是四边形ABCD四条边的中点,若EFGH为菱形,则四边形应具备的下列条件中,不正确的个数是( )
①一组对边平行而另一组对边不平行; ②对角线互相平分;③对角线互相垂直;④对角线相等
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.

(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
 +(﹣3x2+5x﹣7)=﹣2x2+3x﹣6
+(﹣3x2+5x﹣7)=﹣2x2+3x﹣6(1)求所捂的多项式;
(2)若x是
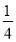 x=﹣
x=﹣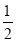 x+3的解,求所捂多项式的值;
x+3的解,求所捂多项式的值;(3)若x为正整数,x每取一个值,都可以求出所捂多项式的值,请你任取x的几个值(不要写在答题纸上),发现它们之间有一定的规律,请用含x的式子表示这一结论:____________=_____________;
(4)若所捂多项式的值为729,请直接写出x的取值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,且a≠0,b≠0,a+b≠0,则函数y=ax+b与
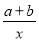 在同一坐标系中的图象不可能是( )
在同一坐标系中的图象不可能是( )A.
 B.
B. 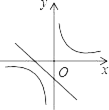
C.
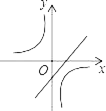 D.
D. 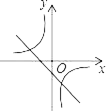
相关试题

