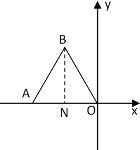
【题目】如图1,等边△OAB的顶点A在x轴的负半轴上,点B(a,b)在第二象限内,且a,b满足![]() .点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
.点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
(1)求点A的坐标;
(2)如图2,当点P在y轴正半轴上时,求点M的坐标;
(3)如图3,当点P在y轴负半轴上时,求出OP,CD,AD满足的数量关系,并证明你的结论.

参考答案:
【答案】(1)A(-4,0);(2)M(4,0);(3)OP= CD+![]() AD,证明见解析.
AD,证明见解析.
【解析】
(1)如图1中,作BN⊥AO于N.由非负数的性质求出点B坐标即可解决问题;
(2)只要证明△ABC≌△AOP,得出∠ABC=∠AOP=90°,在Rt△ABM中,解直角三角形即可解决问题;
(3)如图3中,取AD的中点R,连接BR、OR.首先证明A、B、D、O四点共圆,推出∠BAD=∠BOD=90°-60°=30°,可得BD=![]() AD,再证明△OAP≌△BAC,可得OP=BC=CD+BD=CD+
AD,再证明△OAP≌△BAC,可得OP=BC=CD+BD=CD+![]() AD.
AD.
(1)如图1中,作BN⊥AO于N.
∵![]() ,
,
∴a=-2,b=2![]() ,
,
∴B(-2,2![]() ),
),
∵BA=BO,BN⊥OA,
∴NA=NO=2,
∴OA=4,
∴A(-4,0).
(2) 如图2中,
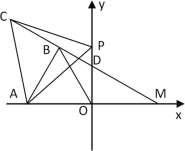
∵△ABO,△APC都是等边三角形,
∴∠OAB=∠PAC,OA=OB,AP=AC,
∴∠OAP=∠BAC,
∴△OAP≌△BAC,
∴∠AOP=∠CBA=90°,
在Rt△ABM中,∵∠ABM=90°,AB=OA=4,∠BAM=60°,
∴AM=2AB=8,
∴OM=AM-OA=4,
∴M(4,0).
(3) 结论:OP=CD+![]() AD.
AD.
理由:如图3中,取AD的中点R,连接BR、OR.
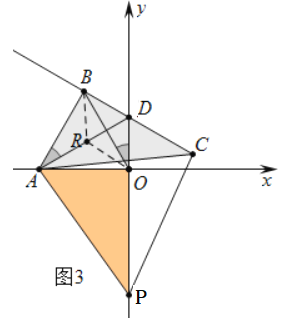
∵∠ABD=∠AOD=90°,AR=DR,
∴BR=AR=RD=OR,
∴A、B、E、O四点共圆,
∴∠BAD=∠BOD=90°-60°=30°,
∴BD=![]() AD,
AD,
∵△ABO,△APC都是等边三角形,
∴∠OAB=∠PAC,OA=OB,AP=AC,
∴∠OAP=∠BAC,
∴△OAP≌△BAC,
∴OP=BC=CD+BD=CD+![]() AD.
AD.
即OP=CD+![]() AD.
AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
-
科目: 来源: 题型:
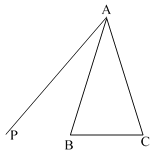
查看答案和解析>>【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
∵
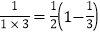 ,
,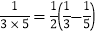 ,
,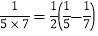 ,……
,……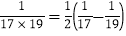 ,
,∴
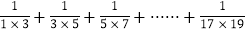
=
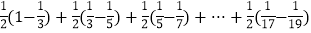
=
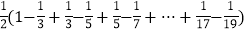 =
=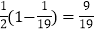 .
.解答下列问题:
(1)在和式
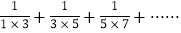 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.(2)上述求和的想法是通过逆用________法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
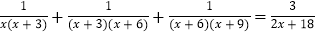 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
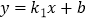 (
( 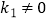 )与反比例函数
)与反比例函数 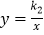 (
( 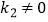 )的图象交于点
)的图象交于点 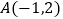 ,
, 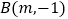 .
.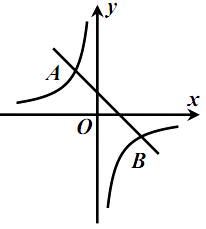
(1)求这两个函数的表达式;
(2)在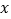 轴上是否存在点
轴上是否存在点 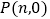
 ,使
,使 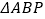 为等腰三角形?若存在,求
为等腰三角形?若存在,求 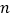 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。

根据以上信息,解答下列问题:
(1)设租车时间为 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为  元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为  元,分别求出
元,分别求出  ,
,  关于
关于  的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
相关试题

