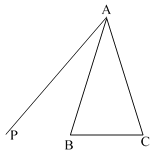
【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.
参考答案:
【答案】(1)补图见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据要求画出图象即可;
(2)根据点B、D关于AP对称得AP垂直平分BD,故ED=EB,从而得证;
(3)连接AD,由线段垂直平分线的性质得AD=AB,ED=EB,可证∠1=∠ABE;由AB=AC得AD=AC,所以∠1=∠ACE,从而得证.
(1)如图;
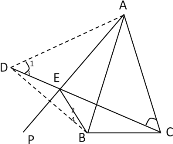
(2)∵ 点B、D关于AP对称
∴ AP垂直平分BD
∴ ED=EB
∴ CD=CE+ED=CE+EB;
(3)连接AD
∵ AP垂直平分BD
∴ AD=AB=AC
∴ ∠1=∠ACE ∠1+∠EDB=∠ABE +∠EBD
∵ ED=EB
∴ ∠EDB =∠EBD
∴ ∠1=∠ABE
∴ ∠ABE=∠ACE .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织学生乘汽车去自然保护区野营,先以60km/h的速度走平路,后又以30km/h的速度爬坡,共用了6.5h;原路返回时,汽车以40km/h的速度下坡,又以50km/h的速度走平路,共用了6 h。问平路和坡路各有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
∵
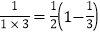 ,
,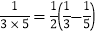 ,
,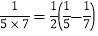 ,……
,……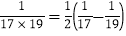 ,
,∴
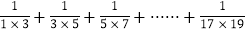
=
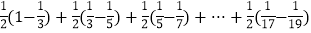
=
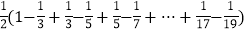 =
=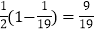 .
.解答下列问题:
(1)在和式
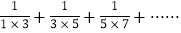 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.(2)上述求和的想法是通过逆用________法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
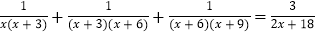 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边△OAB的顶点A在x轴的负半轴上,点B(a,b)在第二象限内,且a,b满足
 .点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
.点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.(1)求点A的坐标;
(2)如图2,当点P在y轴正半轴上时,求点M的坐标;
(3)如图3,当点P在y轴负半轴上时,求出OP,CD,AD满足的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
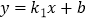 (
( 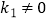 )与反比例函数
)与反比例函数 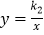 (
( 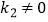 )的图象交于点
)的图象交于点 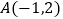 ,
, 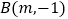 .
.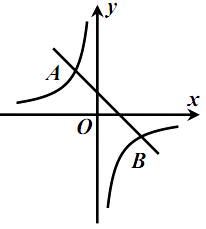
(1)求这两个函数的表达式;
(2)在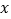 轴上是否存在点
轴上是否存在点 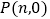
 ,使
,使 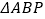 为等腰三角形?若存在,求
为等腰三角形?若存在,求 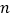 的值;若不存在,说明理由.
的值;若不存在,说明理由.
相关试题

