【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
参考答案:
【答案】
(1)
解:设解析式为:y=kx+b,
将(1,0),(0,﹣2)代入得: ![]() ,
,
解得: ![]() ,
,
∴这个函数的解析式为:y=﹣2x+2;
把x=﹣2代入y=﹣2x+2得,y=6,
把x=3代入y=﹣2x+2得,y=﹣4,
∴y的取值范围是﹣4≤y<6
(2)
解:∵点P(m,n)在该函数的图象上,
∴n=﹣2m+2,
∵m﹣n=4,
∴m﹣(﹣2m+2)=4,
解得m=2,n=﹣2,
∴点P的坐标为(2,﹣2)
【解析】(1)利用待定系数法求一次函数解析式得出即可;再利用一次函数增减性得出y的范围即可.(2)根据题意得出n=﹣2m+2,联立方程,解方程即可求得.
【考点精析】关于本题考查的一次函数的性质和解二元一次方程组,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;二元一次方程组:①代入消元法;②加减消元法才能得出正确答案.
-
科目: 来源: 题型:
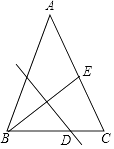
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
A.x﹣y2=3
B.2x﹣y2=9
C.3x﹣y2=15
D.4x﹣y2=21 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表组别(m)
频数
1.09~1.19
8
1.19~1.29
12
1.29~1.39
A
1.39~1.49
10

(1)求A的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.

(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.

(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
相关试题

