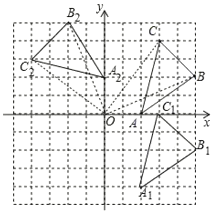
【题目】在平面直角坐标系中,△ABC 的位置如图所示:(每个小方格都是边长为 1 个单位长度的正方形)
(1)将△ABC 沿 y 轴方向向下平移 4 个单位长度得到![]() 则点
则点 ![]() 坐标为_______;
坐标为_______;
(2)将△ABC 绕着点 O 逆时针旋转 90°,画出旋转后得到的![]() ;
;
(3)直接写出点![]() ,
,![]() 的坐标.
的坐标.

参考答案:
【答案】(1)(3,0);(2)![]() 如图所示;(3)点B2,C2的坐标分别为(2,5),(4,3).
如图所示;(3)点B2,C2的坐标分别为(2,5),(4,3).
【解析】
(1)利用平移方向和距离得到A1、B1、C1的位置,然后顺次连接得到![]() ,写出
,写出![]() 坐标即可;
坐标即可;
(2)利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2,从而得到△A2B2C2;
(3)利用(2)中所画图形写出点B2,C2的坐标.
解:(1)如图,![]() 即为所作,点C1坐标为(3,0);
即为所作,点C1坐标为(3,0);
故答案为(3,0);
(2)如图,![]() 即为所作;
即为所作;
(3)点B2,C2的坐标分别为(2,5),(4,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).

(1)当x为何值时,PQ∥BC;
(2)当△APQ与△CQB相似时,AP的长为________.;
(3)当S△BCQ:S△ABC=1:3,求S△APQ:S△ABQ的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(2,0),∠ABO=30°,且AB⊥BC.

(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为


如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,

 ,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21,
,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数-23,-22,-21, ,求图4中所有圆圈中各数的绝对值之和.
,求图4中所有圆圈中各数的绝对值之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,
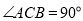 ,点P为AC边上一点,将线段AP绕点A顺时针方向旋转,当AP旋转至
,点P为AC边上一点,将线段AP绕点A顺时针方向旋转,当AP旋转至 时,点
时,点 恰好在同一直线上,此时
恰好在同一直线上,此时 于点E.
于点E.
(1)求证:

(2)若
 ,求AE的长
,求AE的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点
 、
、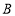 、
、 都是格点.
都是格点.
(1)将
 向左平移6个单位长度得到
向左平移6个单位长度得到 ;
;(2)将
 绕点
绕点 按逆时针方向旋转180°得到
按逆时针方向旋转180°得到 ,请画出
,请画出 ;
;(3)若点
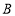 的坐标为(3,3);写出
的坐标为(3,3);写出 与
与 的对称中心的坐标_____.
的对称中心的坐标_____.
相关试题

