Question

【题目】如图，在Rt△ABC中，,点P为AC边上一点，将线段AP绕点A顺时针方向旋转,当AP旋转至时，点恰好在同一直线上，此时于点E．

(1)求证：

(2)若,求AE的长

Answer 1

【答案】（1）详见解析；（2）3

【解析】

（1）根据旋转的性质可得AP=AP′，根据等边对等角的性质可得∠APP′=∠AP′P，再根据等角的余角相等证明即可；
（2）过点P作PD⊥AB于D，根据角平分线上的点到角的两边的距离相等可得CP=DP，然后求出∠PAD=∠AP′E，利用“角角边”证明△APD和△P′AE全等，根据全等三角形对应边相等可得AE=DP，然后求得AE的长即可；

证明：（1）∵AP′是AP旋转得到，
∴AP=AP′，
∴∠APP′=∠AP′P，
∵∠C=90°，AP′⊥AB，
∴∠CBP+∠BPC=90°，∠ABP+∠AP′P=90°，
又∵∠BPC=∠APP′
∴∠CBP=∠ABP；

（2）如图，过点P作PD⊥AB于D，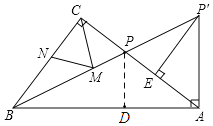

又∵∠CBP=∠ABP，∠C=90°，
∴CP=DP，
∵P′E⊥AC，
∴∠EAP′+∠AP′E=90°，
又∵∠PAD+∠EAP′=90°，
∴∠PAD=∠AP′E，
在△APD和△P′AE中，
，
∴△APD≌△P′AE（AAS），
∴AE=DP，
∴AE=CP，
∵AB-BC=4，AC=8，

设AB=m,则BC=m-4，

在Rt△PDA中，

，

解得：m=10，

∴AB=10，BC=6，
设PC=PD=x，则AD=10-6=4，PA=8-x，
在R t △PDA中，x2+42=（8-x）2，
解得x=3，
∴AE=CP=3；