【题目】某种产品的年产量不超过1 000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣费用)
参考答案:
【答案】解:设年产量为t吨,费用为y(万元),每吨销售价为z(万元),则0≤t≤1000,
由图(1)可求得y=10t,
由图(2)求得z=﹣ ![]() t+30.
t+30.
设毛利润为w(万元),
则w=tz﹣y=t(﹣ ![]() t+30)﹣10t=﹣
t+30)﹣10t=﹣ ![]() t2+20t.
t2+20t.
∴﹣ ![]() t2+20t=7500,
t2+20t=7500,
∴t2﹣2000t+750000=0,
解得t1=500,t2=1500(不合题意,舍去).
故年产量是500吨时,当年可获得7500万元毛利润.
【解析】(1)先观察函数图像,根据图像上的点的坐标,利用待定系数法求出两函数的解析式。然后设毛利润为w(万元),根据毛利润=销售额﹣费用。得出w=tz﹣y,列出w与t的函数关系式,根据w=7500,建立方程求解,再根据某种产品的年产量不超过1 000吨,得出t的值。,
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD.

(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,F是
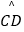 上一点,且
上一点,且 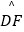 =
= 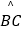 ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) 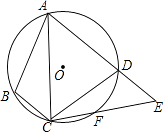
A.45°
B.50°
C.55°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是 .
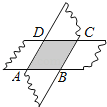
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)完成下面的推理说明:
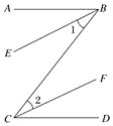
已知:如图,BE∥CF,BE、CF分别平分∠ABC和∠BCD.求证:AB∥CD.
(2)说出(1)的推理中运用了哪两个互逆的真命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
(1)求证:MD和NE互相平分;
(2)若BD⊥AC,EM=2
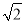 ,OD+CD=7,求△OCB的面积.
,OD+CD=7,求△OCB的面积.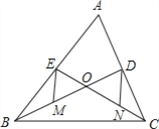
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,F是
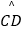 上一点,且
上一点,且 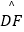 =
= 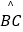 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( ) 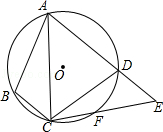
A.60°
B.55°
C.50°
D.45°
相关试题

