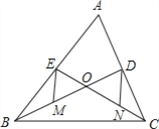
【题目】如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
(1)求证:MD和NE互相平分;
(2)若BD⊥AC,EM=2![]() ,OD+CD=7,求△OCB的面积.
,OD+CD=7,求△OCB的面积.
参考答案:
【答案】(1)见试题解析(2)8.5.
【解析】试题分析:(1)连接ED、MN,根据三角形中位线定理可得ED∥MN,ED=MN,进而得到四边形DEMN是平行四边形,再根据平行四边形的性质可得MD和NE互相平分;
(2)利用(1)中所求得出OC=2DN=4![]() ,再利用勾股定理以及三角形面积公式求出S△OCB=
,再利用勾股定理以及三角形面积公式求出S△OCB=![]() OB×CD即可.
OB×CD即可.
试题解析:(1)证明:连接ED、MN,
∵CE、BD是△ABC的中线,
∴E、D是AB、AC中点,
∴ED∥BC,ED=![]() BC,
BC,
∵M、N分别为OB、OC的中点,
∴MN∥BC,MN=![]() BC,
BC,
∴ED∥MN,ED=MN,
∴四边形DEMN是平行四边形,
∴MD和NE互相平分;
(2)解:由(1)可得DN=EM=2![]() ,
,
∵BD⊥AC,
∴∠ODC=90°,
∵N是OC的中点,
∴OC=2DN=4![]() (直角三角形斜边中线等于斜边的一半)
(直角三角形斜边中线等于斜边的一半)
∵OD2+CD2=OC2=32,
(OD+CD)2=OD2+CD2+2OD×CD=72=49,
2OD×CD=49﹣32=17,
OD×CD=8.5,
∵OB=2OM=2OD,
∴S△OCB=![]() OB×CD=OD×CD=8.5.
OB×CD=OD×CD=8.5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ;点P表示的数是 (用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段MN的长.
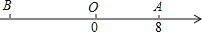
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的不断发展,人与人的沟通方式也发生了很大的变化,盘锦市某中学九年级的一个数学兴趣小组在本年级学生中进行“学生最常用的交流方式”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为四类:A.面对面交谈;B.微信和QQ等聊天软件交流;C.短信与书信交流;D.电话交流.根据调查数据结果绘制成以下两幅不完整的统计图:

(1)本次调查,一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)若该年级有学生150名,请根据调查结果估计这些学生中以“D.电话交流”为最常用的交流方式的人数约为多少?
(3)在本次调查中以“C.短信与书信交流”为最常用交流方式的几位同学中随机抽取两名同学参加盘锦市中学生书信节比赛,请用列举法求所抽取的两名同学都是男同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】至少有两边相等的三角形是( )
A.等边三角形
B.等腰三角形
C.等腰直角三角形
D.锐角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】在1, 0,-1,-2这四个数中,最小的数是( )
A. -2 B. -1 C.0 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+3x-a=0的一个根是2,则a为_____.
相关试题

