【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) 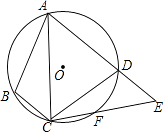
A.45°
B.50°
C.55°
D.60°
参考答案:
【答案】B
【解析】解:∵四边形ABCD内接于⊙O,∠ABC=105°, ∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵ ![]() =
= ![]() ,∠BAC=25°,
,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
故选B.
【考点精析】认真审题,首先需要了解圆心角、弧、弦的关系(在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半),还要掌握圆内接四边形的性质(把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.

A. ① B. ①② C. ①②③ D. 都不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中点,AB=
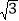 ,AD=2,BC=3,下列结论:
,AD=2,BC=3,下列结论:①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD.

(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是 .
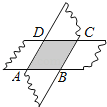
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的年产量不超过1 000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣费用)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)完成下面的推理说明:
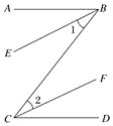
已知:如图,BE∥CF,BE、CF分别平分∠ABC和∠BCD.求证:AB∥CD.
(2)说出(1)的推理中运用了哪两个互逆的真命题.
相关试题

