【题目】如图填空:
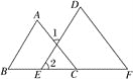
(1)∵∠1=∠A(已知),
∴_________(______________________);
(2)∵∠1=∠D(已知),
∴________(________________________);
(3)∵______=∠F(已知),
∴AC∥DF(______________________).
参考答案:
【答案】AB∥DE 内错角相等,两直线平行 AC∥DF 内错角相等,两直线平行 ∠ACB 同位角相等,两直线平行
【解析】
找出给出的两个角的截线,然后根据平行线的判定进行解答即可.
解:(1)∠1和∠A是由AB、DE被AC所截形成的内错角,
故∵∠1=∠A(已知),
∴AB∥DE(内错角相等,两直线平行);
(2)∠1和∠D是由AC、DF被DE所截形成的内错角,
故∵∠1=∠D(已知),
∴AC∥DF(内错角相等,两直线平行);
(3)AC、DF被BF所截形成的同位角是∠ACB和∠F,
故∵∠ACB=∠F(已知),
∴AC∥DF(同位角相等,两直线平行).
故答案为:(1)AB∥DE,内错角相等,两直线平行;(2)AC∥DF,内错角相等,两直线平行;(3)∠ACB,同位角相等,两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y与x﹣1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)当x=﹣1时,求y的值;
(3)当﹣3<y<5时,求x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
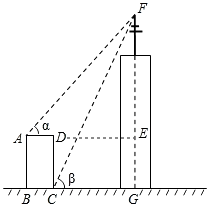
A.(35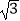 +55)m
+55)m
B.(25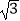 +45)m
+45)m
C.(25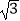 +75)m
+75)m
D.(50+20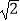 )m
)m -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴和y轴上,OA=3,OB=4.把△AOB绕点A顺时针旋转120°,得到△ADC.边OB上的一点M旋转后的对应点为M′,当AM′+DM取得最小值时,点M的坐标为( )
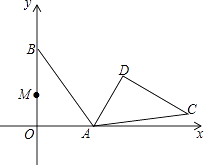
A.(0,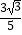 )
)
B.(0, )
)
C.(0,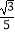 )
)
D.(0,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】给下面命题的说理过程填写依据.
已知:如图,直线AB,CD相交于点O,EO⊥CD,垂足为O,OF平分∠BOD,对∠EOF=
 ∠BOC说明理由.
∠BOC说明理由.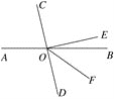
理由:因为∠AOC=∠BOD( ),
∠BOF=
 ∠BOD( ),
∠BOD( ),所以∠BOF=
 ∠AOC( ).
∠AOC( ).因为∠AOC=180°-∠BOC( ),
所以∠BOF=90°-
 ∠BOC.
∠BOC.因为EO⊥CD( ),
所以∠COE=90°( )
因为∠BOE+∠COE=∠BOC( ),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°( )
因为∠EOF=∠BOE+∠BOF( )
所以∠EOF=(∠BOC-90°)+(90°
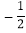 ∠BOC)( )
∠BOC)( )所以∠EOF=
 ∠BOC.
∠BOC. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠C=90°,DE⊥AC于E,交AB于D.
(1)试指出BC、DE被AB所截时,∠3的同位角、内错角和同旁内角;
(2)试说明∠1=∠2=∠3的理由.

-
科目: 来源: 题型:
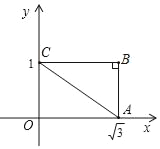
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠ACB=30°,其直角边分别与坐标轴垂直,已知顶点的坐标为A(
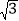 ,0),C(0,1).
,0),C(0,1).(1)如果A关于BC对称的点是D,则点D的坐标为 ;
(2)过点B作直线m∥AC,交CD连线于E,求△BCE的面积.
相关试题

