搜索
【题目】完成下面的证明过程：
已知：如图，∠D=110°，∠EFD=70°，∠1=∠2，
求证：∠3=∠B
证明：∵∠D=110°, ∠EFD=70°（已知）
∴∠D+∠EFD=180°
∴AD∥______（ ）
又∵∠1=∠2(已知)
∴_____∥BC ( 内错角相等，两直线平行)
∴EF∥_____ ( )
∴∠3=∠B(两直线平行，同位角相等)
参考答案：
【答案】详见解析.
【解析】
求出∠D+∠EFD=180°，根据平行线的判定推出AD∥EF，AD∥BC，即可推出答案．
证明：∵∠D=110°, ∠EFD=70°（已知）
∴∠D+∠EFD=180°
∴AD∥_EF_（ 同旁内角互补，两直线平行 ）
又∵∠1=∠2(已知)
∴AD∥BC ( 内错角相等，两直线平行)
∴EF∥_BC_ ( 平行于同一直线的两直线平行 )
∴∠3=∠B(两直线平行，同位角相等) ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，直线y=x+m与y=
在第一象限交于点A，且与x轴交于点C，AB⊥x轴，垂足为B，且S△AOB=1．
（1）求m的值；
（2）求△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去，……，已知正方形ABCD的面积为S1为1，按上述方法所作的正方形的面积依次为S2，S3，……………，则Sn（n为正整数），那么第n个正方形的面积Sn等于（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地区为了进一步缓解交通拥堵问题，决定修建一条长为7千米的公路．如果平均每天的修建费y（万元）与修建天数x（天）在30≤x≤12 0之间时具有一次函数的关系，如下表所示．
x
50
60
90
120
y
40
38
32
26
（1）求y关于x的函数关系式；
（2）后来在修建的过程中计划发生改变，政府决定多修3千米，因此在没有增减建设力量的情况下，修完这条路比计划晚了15天，求原计划每天的修建费． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在Rt△ABC中，∠ABC=90°，AB=BC， BO是AC边上的中线，点P，D分别在AO和BC上，PB=PD，DE⊥AC于点E，
（1）求证：△BPO≌△PDE．
（2）若PB平分∠ABO，其余条件不变．求证：AP=CD．
（先将图形补充完整，然后再证明）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，一张矩形纸片ABCD，其中AD=8cm，AB=6cm，先沿对角线BD对折，点C落在点C′的位置，BC′交AD于点G．
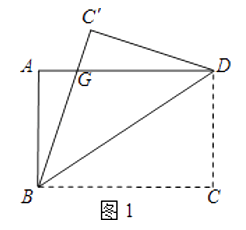
（1）求证：AG=C′G；
（2）如图2，再折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M，求EM的长．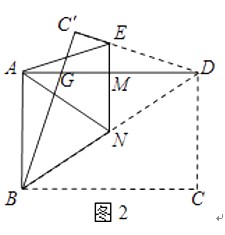
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，点P在AD上，AB=2，AP=1．将直角尺的顶点放在P处，直角尺的两边分别交AB，BC于点E，F，连接EF（如图①）．
（1）当点E与点B重合时，点F恰好与点C重合（如图②），求PC的长；
（2）探究：将直尺从图②中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止．在这个过程中，请你观察、猜想，并解答：
①tan∠PEF的值是否发生变化？请说明理由；
②直接写出从开始到停止，线段EF的中点经过的路线长．
相关试题
