Question

【题目】如图，已知在Rt△ABC中，∠ABC=90°，AB=BC， BO是AC边上的中线，点P，D分别在AO和BC上，PB=PD，DE⊥AC于点E，

（1）求证：△BPO≌△PDE．

（2）若PB平分∠ABO，其余条件不变．求证：AP=CD．

（先将图形补充完整，然后再证明）

Answer 1

【答案】（1）证明见解析；（2）见解析.

【解析】分析：（1）根据等腰三角形的性质和三角形外角的性质可得到∠2=∠1+∠3=∠4+∠C，可得到∠3=∠4，可证明△BPO≌△PDE；（2）由角平分线的定义结合（1）可证得∠ABP=∠4，结合条件可证明△ABP≌△CPD，可证得AP=CD．

本题解析:

(1)证明：∵PB=PD，∴∠2=∠PBD，

∵AB=BC，∠ABC=90°，∴∠A=∠C =45°，

∵AB=BC， BO中线，∴BO⊥AC，∠1= =45°，∴∠1=∠C，

∵∠PBC =∠3+∠1，∠2=∠4+∠C，∴∠3=∠4，

∵BO⊥AC，DE⊥AC，∴∠BOP=∠PED=90°，

在△BPO和△PDE中

∵∠3＝∠4，∠BOP＝∠PED， BP＝PD

∴△BPO≌△PDE（AAS）；

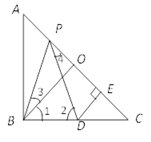
（2）证明：由（1）可得：∠3=∠4，

∵BP平分∠ABO，∴∠ABP=∠3，∴∠ABP=∠4，

在△ABP和△CPD中

∵∠A＝∠C，∠ABP＝∠4，PB＝PD

∴△ABP≌△CPD（AAS）

∴AP=CD．