搜索
【题目】解下列方程组：
（1）
（2）
（3）
（4）
参考答案：
【答案】（1）
（2）
（3）
（4）
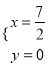
【解析】试题分析:(1)先由
可变形得: 
,把
代入到
可得: 
,解得: 
,把
代入到
可得: 
,
（2）
由
可得: 
,再由
可得: 
,解得
,
将
代入
可得: 
,
（3）由
可得: 
,
把
代入
可得: 
,
解得: 
,把
代入
可得: 
,
(4) 先由
可得: 
,可得
,
由
可得: 
,即
,
由
可得: 
,把
代入
可得
,
试题解析:（1）
,
由
可得: 
,把
代入到
可得: 
,解得: 
,把
代入到
可得: 
,所以方程组的解是
,
（2）
,
由
可得: 
,
由
可得: 
,解得
,
将
代入
可得: 
,
所以方程组的解是
.
（3）
,
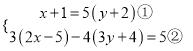由
可得: 
,
把
代入
可得: 
,
解得: 
,把
代入
可得: 
,
所以方程组的解是
.
（4）
,
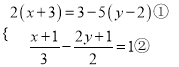由
可得: 
,可得
,
由
可得: 
,即
,
由
可得: 
,把
代入
可得
,
所以方程组的解是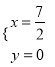
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，BC∥OA，∠B＝∠A＝100°，点E、F在BC上，OE平分∠BOF，且∠FOC＝∠AOC，下列结论中正确的是___________：
①OB∥AC ②∠EOC＝45°
③∠OCB：∠OFB＝1：3 ④若∠OEB＝∠OCA，则∠OCA＝60°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,四边形ABCD,四边形BEFG均为正方形,连接AG,CE.试说明:
(1)AG=CE;
(2)AG⊥CE.
-
科目： 来源： 题型：
查看答案和解析>>【题目】推理填空：如图，已知∠B＝∠CGF，∠DGF＝∠F，求证∠B＋∠F＝180°.
证明：∵∠B= (已知)，
∴AB∥C( )，
∵∠DGF= (已知)，
∴CD∥EF( )，
∴AB∥ ( )
∴∠B+ =180°( ).
-
科目： 来源： 题型：
查看答案和解析>>【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
（1）完成表中填空① ；② ；
（2）请计算甲六次测试成绩的方差；
（3）若乙六次测试成绩方差为
，你认为推荐谁参加比赛更合适，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解题：
定义：如果一个数的平方等于-1，记为i2=-1，这个数i叫做虚数单位，把形如a+bi（a，b为实数）的数叫做复数，其中a叫这个复数的实部，b叫做这个复数的虚部，它的加、减，乘法运算与整式的加、减、乘法运算类似．
例如计算：(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i；
(1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i；
根据以上信息，完成下列问题：
（1）填空：i3= ，i4= ；
（2）计算：(1+i)×(3-4i)；
（3）计算：i+i2+i3+…+i2018．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点
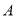是双曲线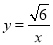 
在第三象限分支上的一个动点，连接 
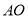并延长交另一分支于点 
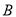，以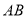 
为边作等边三角形 
，点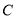 
在第四象限内，且随着点 
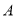的运动，点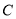 
的位置也在不断变化，但点 
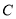始终在双曲线 
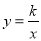上运动，则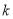 
的值是_______________．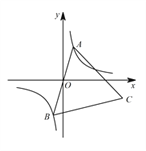
相关试题
