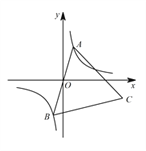
【题目】如图,已知点 ![]() 是双曲线
是双曲线 ![]() 在第三象限分支上的一个动点,连接
在第三象限分支上的一个动点,连接 ![]() 并延长交另一分支于点
并延长交另一分支于点 ![]() ,以
,以 ![]() 为边作等边三角形
为边作等边三角形 ![]() ,点
,点 ![]() 在第四象限内,且随着点
在第四象限内,且随着点 ![]() 的运动,点
的运动,点 ![]() 的位置也在不断变化,但点
的位置也在不断变化,但点 ![]() 始终在双曲线
始终在双曲线 ![]() 上运动,则
上运动,则 ![]() 的值是_______________.
的值是_______________.
参考答案:
【答案】![]()
【解析】因为双曲线 的图象关于原点对称,
所以点 ![]() 与点
与点 ![]() 关于原点对称.
关于原点对称.
所以 ![]() .连接
.连接 ![]() ,如图所示.
,如图所示.
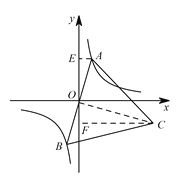
因为 ![]() 是等边三角形,
是等边三角形, ![]() ,
,
所以 ![]() ,
, ![]() .
.
所以 ![]() .
.
所以 ![]() .
.
过点 ![]() 作
作 ![]() 轴,垂足为
轴,垂足为 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴,垂足为
轴,垂足为 ![]() .
.
因为 ![]() ,
, ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() .
.
所以 ![]() .相似比
.相似比 ![]() ,
,
所以面积比 ![]() .
.
因为点 ![]() 在第一象限,设点
在第一象限,设点 ![]() 坐标为
坐标为 ![]() ,
,
因为点 ![]() 在双曲线 上,
在双曲线 上,
所以 ![]() ,
,
所以 ![]() .
.
所以设点 ![]() 坐标为
坐标为 ![]() ,
,
因为点 ![]() 在双曲线
在双曲线 ![]() 上,
上,
所以 ![]() .
.
因为点 ![]() 在第四象限,
在第四象限,
所以 ![]() ,
, ![]() .
.
所以 ![]() .
.
所以 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程组:
(1)
 (2)
(2)
(3)
 (4)
(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为
 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.
例如计算:(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i;
(1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i;
根据以上信息,完成下列问题:
(1)填空:i3= ,i4= ;
(2)计算:(1+i)×(3-4i);
(3)计算:i+i2+i3+…+i2018.
-
科目: 来源: 题型:
查看答案和解析>>【题目】何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0∴m=﹣3,n=3
为什么要对2n2进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程..
解决问题:
(1)若x2﹣4xy+5y2+2y+1=0,求xy的值;
(2)已知a、b、c是△ABC的三边长,满足a2+b2=10a+12b﹣61,c是△ABC中最短边的边长,且c为整数,那么c可能是哪几个数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.(提示:过点B作BM∥AD交EG的延长线于点M,证明EG//AB且EG=
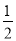 AB)
AB)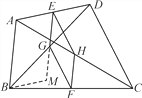
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表所示为装运、销售甲、乙、丙三种蔬菜的重量及利润。某公司计划用20辆汽车装运甲、乙、丙三种蔬菜共36吨到某地销售.规定每辆汽车满载,每车只装一种蔬菜,每种蔬菜不少于一车。应如何安排,可使公司获得利润18300元?
甲
乙
丙
每辆汽车装运的吨数
2
1
1.5
每吨蔬菜可获利润(百元)
5
7
4
相关试题

