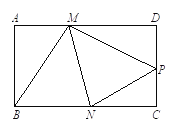
【题目】已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD与点M,折痕交边BC于点N .
(1)写出图中的全等三角形. 设CP= ![]() ,AM=
,AM= ![]() ,写出
,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)试判断∠BMP是否可能等于90°. 如果可能,请求出此时CP的长;如果不可能,请说明理由.
参考答案:
【答案】(1)![]() ;(2)当CM=1时,
;(2)当CM=1时, ![]() .
.
【解析】试题分析:(1)由折叠的性质可得:△MBN≌△MPN,即可得MB=MP,又由四边形ABCD是矩形,可得AB=CD,∠A=∠D=90°,然后分别在Rt△ABM与Rt△DMP中,利用勾股定理,可得MB2=AM2+AB2=y2+4,MP2=MD2+PD2=2+2,继而求得y与x的函数关系式;
(2)若∠BMP=90°,可证得△ABM≌△DMP,即可得AM=DP,AB=DM,则可求得CP的长.
试题解析:(1)⊿MBN≌⊿MPN .
∵⊿MBN≌⊿MPN,
∴MB=MP,
∴![]() .
.
∵矩形ABCD,
∴AD=CD (矩形的对边相等),
∴∠A=∠D=90°(矩形四个内角都是直角) .
∵AD=3, CD=2, CP=x, AM=y,
∴DP=2-x, MD=3-y .
在Rt⊿ABM中,
![]() .
.
同理 ![]() .
.
![]() .
.
∴ ![]() .
.
(2)![]()
当![]() 时,
时,
可证![]() .
.
∴ AM=CP,AB=DM.
∴![]() .
.
∴![]() .
.
∴当CM=1时, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为
 ,这个数
,这个数 叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为 (
( ,
,  为实数),
为实数), 叫这个复数的实部,
叫这个复数的实部,  叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。例如计算:


(1)填空:
 =_________,
=_________,  =____________;
=____________;(2)计算:
 ;
;(3)计算:

-
科目: 来源: 题型:
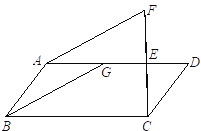
查看答案和解析>>【题目】已知:如图,点E、G在平行四边形ABCD的边AD上,EG=ED,延长CE到点F,使得EF=EC.求证:AF∥BG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员带了2件上衣和3条短裤(上衣和短裤分别装在两个包里),上衣的颜色是红色和白色,短裤的颜色是红色、白色、黄色.
(1)他随意拿出一件上衣和一条短裤配成一套,用画树状图或列表的方法列出所有可能出现的结果.
(2)他随意拿出一件上衣和一条短裤,颜色正好相同的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(
 ,0),B(
,0),B( ,0),且
,0),且 、
、 满足
满足 ,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)请直接写出C,D两点的坐标.
(2)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)
 的值是否发生变化?并说明理由.
的值是否发生变化?并说明理由.(3)在坐标轴上是否存在一点M,使三角形MBC的面积与三角形ACD的面积相等?若存在直接写出点M的坐标,若不存在,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线
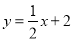 分别交
分别交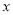 轴、
轴、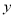 轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥
轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥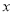 轴,B为垂足,且S⊿ABC= 6.
轴,B为垂足,且S⊿ABC= 6.(1)求点B和P的坐标;
(2)过点B画出直线BQ∥AP,交
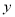 轴于点Q,并直接写出点Q的坐标.
轴于点Q,并直接写出点Q的坐标.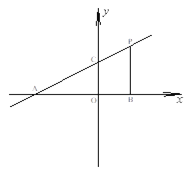
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|x|=5,那么x等于( )
A.5B.-5C.+5或-5D.以上都不对
相关试题

