【题目】如图①,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=40°,求∠DOE的度数;
(2)如图①,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示)
(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,OE平分∠BOC.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC﹣3∠AOF=2∠BOE,试确定∠AOF与∠DOE的度数之间的关系,说明理由.

参考答案:
【答案】(1)20°;(2)∠DOE=![]() ;(3)①∠DOE=
;(3)①∠DOE=![]() ∠AOC,理由见解析;②4∠EOD﹣3∠AOF=180°,理由见解析.
∠AOC,理由见解析;②4∠EOD﹣3∠AOF=180°,理由见解析.
【解析】
首先求得∠COB的度数,然后根据角平分线的定义求得∠COE的度数,再根据∠DOE=∠COD-∠COE即可求解;
解法与(1)相同,把①中的60°改成α即可;
①把∠AOC的度数作为已知量,求得∠BOC的度数,然后根据角的平分线的定义求得∠COE的度数,再根据∠DOE=∠COD-∠COE求得∠DOE,即可解决;
②由∠AOC﹣3∠AOF=2∠BOE, OE平分∠BOC,∠AOC和∠DOE的关系,可以建立各个角之间的关系,从而可以得到∠AOF与∠DOE的度数之间的关系.
(1)∵∠AOC=40°
∴∠COB=180°﹣∠AOC=180°﹣40°=140°
∵OE平分∠COB
∴∠COE=![]() ∠COB=70°,
∠COB=70°,
又∵∠COD=90°
∴∠EOD=∠COD﹣∠COE=20°
(2)∠DOE=![]() ,
,
(3)①∠DOE=![]() ∠AOC,理由如下:
∠AOC,理由如下:
∵OE平分∠COB
∴∠COE=![]() ∠COB
∠COB
又∵∠COD=90°
∴∠EOD=∠COD﹣∠COE=90°﹣![]() ∠COB,
∠COB,
∵∠COB+∠AOC=180°
∴∠COB=180°﹣∠AOC
∴∠EOD=90°﹣![]() (180°﹣∠AOC)=
(180°﹣∠AOC)=![]() ∠AOC
∠AOC
②4∠EOD﹣3∠AOF=180°,理由如下:
∵OE平分∠COB
∴∠EOB=∠COE
∴∠AOC﹣2∠BOE=∠AOC﹣2∠COE
=∠AOC﹣2(90°﹣∠EOD)
=∠AOC+2∠EOD﹣180°
又∵∠DOE=![]() ∠AOC
∠AOC
∴∠AOC﹣2∠BOE=4∠EOD﹣180°
∵∠AOC﹣3∠AOF=2∠BOE
∴4∠EOD﹣3∠AOF=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把
 (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.(1)直接写出计算结果:2③= ,(-3)④ = ,
 ⑤= .
⑤= .(2)计算 24÷23 + (-8)×2③.
-
科目: 来源: 题型:
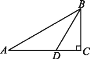
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,则BC的长是 ( )
A. 20 B. 20
 C. 30 D. 10
C. 30 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以O(0,0)、A(2,0)为顶点作正△OAP1 , 以点P1和线段P1A的中点B为顶点作正△P1BP2 , 再以点P2和线段P2B的中点C为顶点作△P2CP3 , …,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.

(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】为完善人口发展战略,我国现已全面提倡实施一对夫妇可生育两个孩子的政策.某中学为了解在校生对父母再生“二胎”的同意情况,在校园内随机调查了部分学生对“二胎”的同意情况(把调查的结果分为四个等级:A非常同意;B:同意;C:无所谓;D:坚决反对),并将调查结果绘成了如下两幅不完整的统计图. 请根据统计图中的信息解答下列问题:
(1)本次被抽样调查的学生有多少人?
(2)将两幅统计图补充完整:
(3)若全校共有3600名学生,估计“非常同意“父母再生“二胎”的大约有多少人?
(4)若从3名“同意”父母生“二胎”和2名“坚决反对”父母生“二胎”的学生中随机抽取两名学生,用树状图或列表法求抽取的两个恰好都“坚决反对”父母生“二胎”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
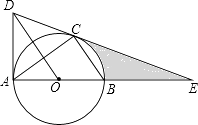
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若AE=6,CE=2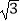 . ①求⊙O的半径
. ①求⊙O的半径
②求线段CE,BE与劣弧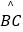 所围成的图形的面积(结果保留根号和π)
所围成的图形的面积(结果保留根号和π)
相关试题

