【题目】每年“双十一”购物活动,商家都会利用这个契机进行打折满减的促销活动.某商家平时的优惠措施是按所有商品标价打七折:“双十一”活动期间的优惠措施是:购买的所有商品先按标价总和打七五折,再享受折后每满![]() 元减
元减![]() 元的优惠.如标价为
元的优惠.如标价为![]() 元的商品,折后为
元的商品,折后为![]() 元,再减
元,再减![]() 元,即实付:
元,即实付:![]() (元).
(元).
(1)该商店标价总和为![]() 元的商品,在“双十一”购买,最后实际支付只需多少元?
元的商品,在“双十一”购买,最后实际支付只需多少元?
(2)小明妈妈在这次活动中打算购买某件商品,打折满减后,应付金额是![]() 元,求该商品的标价.
元,求该商品的标价.
(3)在(2)的条件下,若该商家出售的商品标价均为整数,小明通过计算后告诉妈妈:通过凑单(再购买少量商品)实际支付金额只需再多付 元,就可获得最大优惠?
参考答案:
【答案】(1)![]() 元;(2)
元;(2)![]() 元;(3)只需多付3元,可获得最大优惠
元;(3)只需多付3元,可获得最大优惠
【解析】
(1)根据题意列式计算即可;
(2)设该商品的标价为![]() 元,则折后价为:
元,则折后价为:![]() 元,折后每满
元,折后每满![]() 元减
元减![]() 元的优惠分两种情况讨论,依题意列式计算即可;
元的优惠分两种情况讨论,依题意列式计算即可;
(3)根据题意折后价当![]() 时,可多享受一个折后减
时,可多享受一个折后减![]() 元的优惠,据此求解即可.
元的优惠,据此求解即可.
(1)依题意得:![]() (元),
(元),
∵![]() ,
,
∴可再减:![]() (元),
(元),
实际付款:![]() (元);
(元);
(2)设该商品的标价为![]() 元,则折后价为:
元,则折后价为:![]() 元,
元,
①当![]() 时,
时,
依题意得:![]() ,
,
解得:![]() ,
,
![]() ,
,
符合题意;
②当![]() 时,
时,
依题意得:![]() ,
,
解得:![]() ,
,
![]() ,
,
不符合题意,舍去;
综上,该商品的标价为![]() 元;
元;
(3)∵该商家出售的商品标价均为整数,
当![]() ,即
,即![]() 元时,
元时,
实际付款:![]() (元),
(元),
![]() (元),
(元),![]() (元),
(元),
故只需多付3元,可多获得![]() 元的商品.
元的商品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
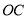 是
是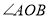 的角平分线,
的角平分线,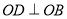 ,
,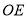 是
是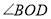 的角平分线,
的角平分线,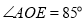
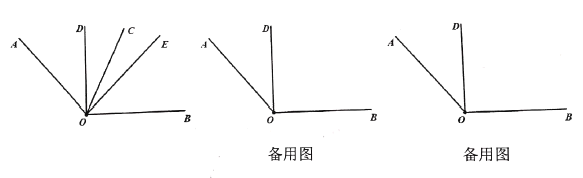
(1)求
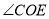 ;
;(2)
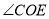 绕
绕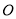 点以每秒
点以每秒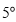 的速度逆时针方向旋转
的速度逆时针方向旋转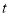 秒(
秒(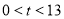 ),
),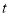 为何值时
为何值时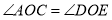 ;
;(3)射线
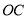 绕
绕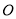 点以每秒
点以每秒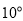 的速度逆时针方向旋转,射线
的速度逆时针方向旋转,射线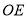 绕
绕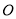 点以每秒
点以每秒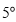 的速度顺时针方向旋转,若射线
的速度顺时针方向旋转,若射线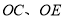 同时开始旋转
同时开始旋转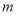 秒(
秒(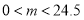 )后得到
)后得到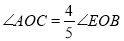 ,求
,求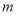 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了从
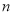 个外形相同的鸡蛋中找出唯一的一个双黄蛋,检查员将这些蛋按
个外形相同的鸡蛋中找出唯一的一个双黄蛋,检查员将这些蛋按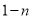 的序号排成一列,第一次先从中取出序号为单数的蛋,发现其中没有双黄蛋;他将剩下的蛋在原来的位置上又按
的序号排成一列,第一次先从中取出序号为单数的蛋,发现其中没有双黄蛋;他将剩下的蛋在原来的位置上又按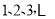 编了序号(即原来的
编了序号(即原来的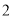 号变为
号变为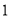 号,原来的
号,原来的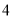 号变为
号变为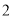 号,
号, ),又从中取出新序号为单数的蛋进行检查,仍没有发现双黄蛋;如此继续下去,检查到最后一个原始编号为
),又从中取出新序号为单数的蛋进行检查,仍没有发现双黄蛋;如此继续下去,检查到最后一个原始编号为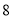 的蛋才是双黄蛋.那么
的蛋才是双黄蛋.那么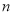 最大值是_________,如果最后找到的是原始编号为
最大值是_________,如果最后找到的是原始编号为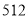 的双黄蛋,则
的双黄蛋,则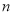 的最大值是_________.
的最大值是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
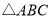 中,
中,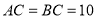 ,
,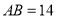 ,将
,将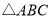 绕点A按顺时针方向旋转得到
绕点A按顺时针方向旋转得到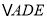 旋转角为
旋转角为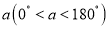 ,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当
,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当 时,点P与点C之间的距离是________.
时,点P与点C之间的距离是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】[阅读理解]射线
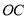 是
是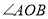 内部的一条射线,若
内部的一条射线,若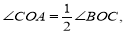 则我们称射线
则我们称射线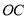 是射线
是射线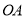 的伴随线.
的伴随线.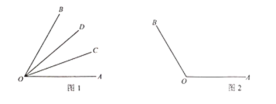
例如,如图1,
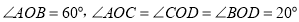 ,则
,则 ,称射线
,称射线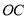 是射线
是射线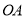 的伴随线:同时,由于
的伴随线:同时,由于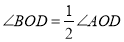 ,称射线
,称射线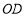 是射线
是射线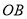 的伴随线.
的伴随线.[知识运用]
(1)如图2,
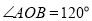 ,射线
,射线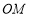 是射线
是射线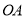 的伴随线,则
的伴随线,则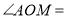 ,若
,若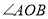 的度数是
的度数是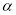 ,射线
,射线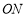 是射线
是射线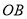 的伴随线,射线
的伴随线,射线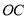 是
是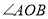 的平分线,则
的平分线,则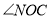 的度数是 .(用含
的度数是 .(用含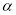 的代数式表示)
的代数式表示)(2)如图,如
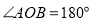 ,射线
,射线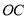 与射线
与射线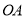 重合,并绕点
重合,并绕点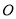 以每秒
以每秒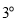 的速度逆时针旋转,射线
的速度逆时针旋转,射线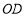 与射线
与射线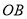 重合,并绕点
重合,并绕点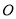 以每秒
以每秒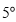 的速度顺时针旋转,当射线
的速度顺时针旋转,当射线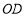 与射线
与射线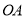 重合时,运动停止,现在两射线同时开始旋转.
重合时,运动停止,现在两射线同时开始旋转.
①是否存在某个时刻
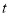 (秒),使得
(秒),使得 的度数是
的度数是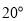 ,若存在,求出
,若存在,求出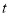 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;②当
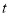 为多少秒时,射线
为多少秒时,射线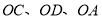 中恰好有一条射线是其余两条射线的伴随线.
中恰好有一条射线是其余两条射线的伴随线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F分别在x轴,y轴的正半轴上.点
 在线段EF上,过A作
在线段EF上,过A作 分别交x轴,y轴于点B,C,点P为线段AE上任意一点(P不与A,E重合),连接CP,过E作
分别交x轴,y轴于点B,C,点P为线段AE上任意一点(P不与A,E重合),连接CP,过E作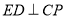 ,交CP的延长线于点G,交CA的延长线于点D.有以下结论①
,交CP的延长线于点G,交CA的延长线于点D.有以下结论① ,②
,② ,③
,③ ,④
,④ ,其中正确的结论是_____.(写出所有正确结论的番号)
,其中正确的结论是_____.(写出所有正确结论的番号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=
 .
.(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
 +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
相关试题

